轴向力偏心距增大系数→轴向力偏心距增大系数

由上述可知，计算各类钢筋混凝土杆系结构中的偏心受压构件的承载力时，应考虑二阶效应引起的偏心距增大值Δ 或附加弯矩NΔ（通常又称为二阶弯矩）。根据工程设计的不同要求，可分别采用精确法或近似法进行计算。

精确法——根据材料的本构关系（应力-应变关系），应用截面中的平衡条件和应变协调条件（平截面假定）以及各节点处的变形协调条件，对结构进行非线性分析，求出在承载能力极限状态下各个截面的内力（包括二阶效应）。这种方法还能同时反映出细长柱可能产生非线性失稳的特性。由于这种计算方法较为复杂，需借助计算机进行，故只在某些特殊的杆系结构的二阶效应分析中才采用。

近似法——首先用两端铰支、作用着等偏心距的轴向压力的构件进行试验，根据试验结果，并结合理论分析，导出在承载能力极限状态下构件中点的轴向力偏心距增大系数η的计算公式，公式中含有构件的计算长度l0（对于两端铰支构件，l0 系指构件的长度）的平方项。然后，通过对各种杆系结构变形特性的分析（考虑轴向力二阶效应），求出各构件中与两端铰支、作用着等偏心距轴向压力构件的变形特性相当的等效长度，并把这一等效长度视为构件的计算长度，代入η的计算公式，以求得该结构各构件临界截面的弯矩（包括二阶弯矩）。

目前，在一般情况下，对于二阶效应的计算可采用近似法。

当按近似法考虑二阶效应对偏心受压构件承载力的影响时，为了确定极限状态下临界截面上轴向压力的实际偏心距，可在轴向力偏心距e0 上叠加以构件弯曲产生的偏心距增大值，也就是临界截面处的构件挠度Δ。因此，轴向力实际偏心距可表示为

令为轴向力偏心距增大系数，则公式（7-11）可改写为

对于轴向力偏心距增大值Δ 或偏心距增大系数η，《规范》系按下述方法确定。

对于两端铰支等偏心距受压柱，其偏心距增大系数η的计算方法如下。

首先，由柱极限状态时临界截面的曲率，直接求临界截面处的挠度Δ，然后再由公式（7-11）计算η。

由材料力学可知

式中 φu——偏心受压构件临界截面的曲率；

l0——偏心受压构件的计算长度；

β——挠度系数。

于是，ηns可按下列公式计算：

根据平截面假定，可求得当截面为界限破坏时极

限曲率φub为（图7-13）

式中 εcu——界限破坏时截面受压区边缘混凝土的极限压应变；

εy——界限破坏时受拉钢筋的拉应变，即εy=fy／Es。

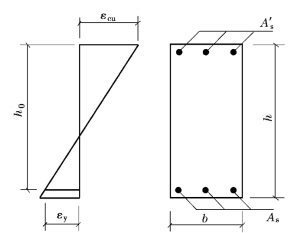
图7-13 临界截面界限破坏时的应变状态

试验表明，轴向力偏心率对偏心受压构件临界截面的极限曲率有一定的影响。因此，在公式（7-15）中乘以系数ζc（考虑轴向力偏心率对截面曲率的影响系数）进行修正。于是可得偏心受压构件临界截面的极限曲率φu 为

将公式（7-15a）代入公式（7-14），且取εcu=0.0033，εy=0.002，则可得

挠度系数β与沿构件长度方向的曲率分布有关。当曲率分布曲线为矩形时，β=8；为三角形时，β=12；为正弦曲线时，β=10。实际构件的曲率分布曲线可认为介于三角形和矩形之间的某种曲线，故近似取β=10。又近似取，则由公式（7-16）可得

当考虑荷载长期作用影响时，可将εcu乘以系数1.25，则可得

当用M2／N 代替e02时，则公式（7-16b）可改写为(www.xing528.com)

ζc 按下列公式计算：

式中 ζc——截面曲率修正系数，当ζc＞1.0时，取ζc=1.0。

按照《规范》规定，计算偏心受压构件承载力时，应计入附加偏心距ea（详见下节），则公式（7-17）可改写为

对于I形、T 形、环形和圆形截面，η也可采用类似的方法确定。ηns仍可按公式（7-18）计算，只需将公式中的h0 和h用相应的截面有效高度和截面高度（或直径）代替即可。

公式（7-17）和（7-18）是根据杆件两端轴向力偏心距相等的情况导出的。试验研究表明，对于杆件两端轴心力偏心距不等的情况，必须进行修正。

根据试验研究结果和借鉴国外有关规范，《规范》规定，除排架结构柱以外的偏心受压构件，在其偏心方向上考虑杆件自身挠曲影响的控制截面弯矩设计值可按下列公式计算：

即

式中 Cm——柱端截面偏心弯矩调节系数；

ηns——弯矩增大系数，又可称为偏心距增大系数。

在经典弹性解析解的基础上，考虑了钢筋混凝土柱非弹性性能的影响，并根据有关的试验资料，《规范》规定，Cm 可按下列公式计算：

式中 M1、M2——分别为偏心受压构件两端截面按结构分析确定的对同一主轴的弯矩设计值，绝对值较大端为M2，绝对值较小端为M1；当构件为单曲率时，M1／M2 为正值，否则为负值。

根据国内对不同杆端弯矩比、不同轴压比和不同长细比的杆件进行的分析计算结果表明，当柱端弯矩比不大于0.9且轴压比不大于0.9时，若杆件长细比满足一定的要求，则考虑杆件自身挠曲后中间区段截面的弯矩值一般不会超过杆端弯矩，即可以不考虑该方向自身挠曲产生的附加弯矩影响。因此，《规范》规定，弯矩作用平面内截面对称的偏心受压构件，当同一主轴方向的杆端弯矩比不大于0.9且设计轴压比（即）不大于0.9时，若构件长细比满足公式（5-21）的要求，可不考虑该方向构件自身挠曲产生的附加弯矩影响。

式中 l0——构件的计算长度，可近似取偏心受压构件相应主轴方向两支撑点之间的距离；

i——偏心方向的截面回转半径；

对于排架结构，由于作用在排架结构上绝大多数荷载都会引起排架的侧移，因此，可以近似用P-Δ 效应增大系数ηs 统乘引起排架侧移荷载产生的端弯矩Ms 与不引起排架侧移荷载产生的端弯矩Mns之和，即

《规范》还规定，排架结构中的ηs 可按下列公式计算：

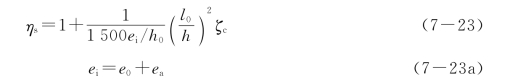
式中 ζc——截面曲率修正系数；按公式（7-17a）计算，当ζc＞1.0时，取ζc=1.0；

ea——附加偏心距；

e0——轴向压力对截面偏心中心的偏心距；

ei——初始偏心距；

l0——柱的计算长度；

h、h0——分别为所考虑弯曲方向柱的截面高度和截面有效高度；

A——柱的截面面积，对于I形截面，A=bh+2（b′f-b）h′f。