纯扭构件扭曲截面承载力计算方法

1）基本计算公式

（1）矩形截面

试验表明，受扭构件开裂以后，由于钢筋的约束，裂缝开展受到一定的限制，增加了骨料之间的咬合力，使混凝土具有一定的抗扭能力。同时，受扭裂缝往往是许多分布在四个侧面上相互平行、断断续续、前后交错的斜裂缝（图6-4）。这些斜裂缝只从表面向内延伸到一定的深度，而不会贯穿整个截面，最终也不完全形成连续的、通长的螺旋形裂缝。因此，混凝土仍然可承担一部分扭矩。由此可见，钢筋混凝土构件的受扭承载力不仅与钢筋的抗扭能力有关，也与混凝土的抗扭能力有关。

根据国内大量的试验研究，《规范》建议按下列经验公式计算矩形截面纯扭构件的受扭承载力（图6-5）：

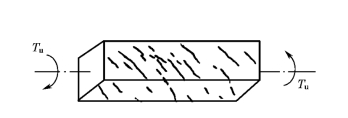
图6-4 纯扭构件的裂缝分布

式中 T——扭矩设计值；

Tu——构件受扭承载力设计值；

Ast1——受扭计算中，沿截面周边所配置箍筋的单肢截面面积；

fyv——箍筋的抗拉强度设计值；

s——沿构件长度方向的箍筋间距；

Acor——截面核心部分的面积bcorhcor；

bcor——截面核心部分的短边尺寸，按箍筋内表面计算；

hcor——截面核心部分的长边尺寸，按箍筋内表面计算；

ft——混凝土抗拉强度设计值；

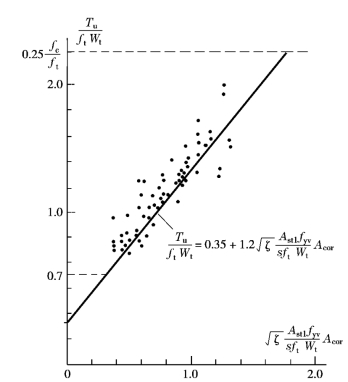
图6-5 矩形截面钢筋混凝土纯扭构件承载力计算公式与试验结果的比较

Wt——截面受扭塑性抵抗矩；

ζ——受扭构件纵向钢筋与箍筋配筋强度的比值；

Astl——受扭计算中取对称布置的全部纵向钢筋截面面积；

fy——纵向钢筋抗拉强度设计值；

ucor——截面核心部分的周长，其取值为2（bcor+hcor）。

公式（6-5）中的ζ应符合下列条件：

当ζ＞1.7时，取ζ=1.7。

钢筋混凝土矩形截面受扭构件的截面尺寸如图6-6a所示。

图6-6 混凝土受扭构件截面尺寸

试验表明，由于纵筋与箍筋间的内力重分布，构件内的纵筋与箍筋配筋强度的比值ζ可在一定范围内变化。当0.6≤ζ≤1.7时，所配置的纵筋和箍筋基本上都能达到屈服。但当ζ=1.2左右时，纵筋和箍筋能够更好地同时达到屈服。所以，设计时一般可取ζ=1.2。还须指出，箍筋用量愈多，施工愈复杂，故设计时一般以纵筋用量略多一些较为合理。因此，当箍筋间距过密时，也可在上述范围内调整ζ的取值，适当减少箍筋用量，增加纵筋用量，以方便施工。

（2）T 形和I形截面

计算T 形、I形截面纯扭构件的受扭承载力时，也可和计算抗裂扭矩一样，将截面划分为几个矩形截面（图6-3），并将扭矩T 按各个矩形分块的受扭塑性抵抗矩分配给各个矩形分块，以求得各个矩形分块所承担的扭矩。各个矩形分块所承担的扭矩可按下列公式计算（I形截面的截面尺寸如图6-6b所示）：

对于腹板部分矩形分块

对于上翼缘矩形分块

对于下翼缘矩形分块

式中 T——构件截面所承受的扭矩设计值；

Tw——腹板所承受的扭矩设计值；

——上翼缘、下翼缘所承受的扭矩设计值。

根据公式（6-8）～公式（6-10），各个矩形分块的钢筋所承担的扭矩按下列公式计算：

对于腹板部分矩形截面，钢筋所承担的扭矩为

即

对于上翼缘矩形截面，钢筋所承担的扭矩为

即

对于下翼缘矩形截面，钢筋所承担的扭矩为

即

公式（6-11）～公式（6-13）表明，对于T 形、I形等组合截面，可将钢筋所承担的扭矩（T-0.35ftWt）按各个矩形分块的受扭塑性抵抗矩分配给各个矩形分块的钢筋来承担。

对于配有封闭箍筋的翼缘，其截面受扭承载力随翼缘悬挑宽度的增加而提高。当悬挑宽度过小，其提高效果不显著。反之，悬挑宽度过大，翼缘与腹板连接时整体刚度减弱，同时，翼缘由于受弯曲而容易断裂，翼缘的抗扭作用将显著降低。因此，《规范》规定，计算的翼缘悬挑宽度应取不大于其高度的3 倍，亦即计算时取用的翼缘宽度应符合和bf≤b+6hf 的规定。同时，其翼缘高度也不宜小于60mm。此外，当或Wtf／Wtw小于0.1时，翼缘的抗扭钢筋可按构造要求配置。

（3）箱形截面

试验和理论分析表明，一定壁厚的箱形截面的受扭承载力可采用与实心截面相同的公式进行计算。同时，当壁厚较小时，将实心矩形截面构件受扭承载力计算公式中的混凝土项乘以与截面相对壁厚有关的折减系数（2.5tw／bh），于是可得（箱形截面的截面尺寸如图6-6c所示）

式中 tw——箱形截面侧壁厚度；

αh——箱形截面壁厚影响系数，αh=2.5 tw／bh，当αh＞1.0时，取αh=1.0。

计算中bh 应取箱形截面的短边尺寸；ζ值应按公式（6-6）计算，且应符合0.6≤ζ≤1.7的要求，当ζ＞1.7时，取ζ=1.7。(www.xing528.com)

2）抗扭配筋的上限和下限

（1）抗扭配筋的上限

如6.2.2节所述，当配筋过多时，受扭构件可能在抗扭钢筋屈服以前便由于混凝土被压碎而破坏。这时，即使进一步增加钢筋，构件所能承担的破坏扭矩几乎不再增大。

因此，《规范》规定，对h／b＜6的矩形、T 形、I形截面和hw／tw＜6的箱形截面钢筋混凝土纯扭构件，其截面应符合下列要求：

当hw／b（或hw／tw）≤4时

当hw／b（或hw／tw）=6时

当4＜hw／b（或hw／tw）＜6时，按线性内插法确定。

式中 T——扭矩设计值；

Wt——纯扭构件的截面受扭塑性抵抗矩；

b——矩形截面的宽度，T 形或I形截面腹板宽度，箱形截面侧壁总厚度2tw；

βc——混凝土强度影响系数，当混凝土强度等级不超过C50时，取βc=1.0，当混凝土强度等级为C80时，取βc=0.8，其间按线性内插法取用；

hw——截面的腹板高度，对矩形截面，取有效高度h0，对T 形截面，取有效高度减去翼缘高度，对I形和箱形截面，取腹板净高；

tw——箱形截面壁厚，其值不应小于bh／7，此处，bh 为箱形截面的宽度。

（2）抗扭配筋的下限

如前面所述，当配筋过少或过稀时，配筋将无助于开裂后构件的抗扭能力，因此，为了防止纯扭构件在低配筋时混凝土发生脆断，应使配筋纯扭构件所能承担的扭矩不小于其抗裂扭矩。根据这一原则和试验结果的分析，《规范》规定，纯扭构件的最小配箍率和纵向受力钢筋的最小配筋率按下列公式确定：

式中 Asv——配置在同一截面内箍筋各肢的全部截面面积。

式中 ρtl——受扭纵向钢筋配筋率，ρtl=Astl／（bh）；

ρtl，min——受扭纵向钢筋最小配筋率。

当作用于构件上的扭矩小于构件的抗裂扭矩时，该扭矩将由混凝土承担。于是，《规范》规定，对于h／b＜6的矩形、T 形、I形截面和hw／tw＜6的箱形截面钢筋混凝土纯扭构件，当符合公式（6-19）的条件时，可按构造要求配置抗扭钢筋。

例题6-1 钢筋混凝土矩形截面纯扭构件的截面尺寸b×h=200mm×300mm，承受扭矩设计值T=9.3kN·m，纵向钢筋混凝土保护层厚度cs=30mm。混凝土强度等级为C30（fc=14.3N／mm2，ft=1.43N／mm2），纵向钢筋和箍筋均采用HRB400级钢筋（fy=fyv=360N／mm2），试计算其配筋。

解 （1）验算构件截面尺寸

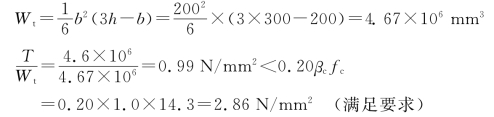
（2）抗扭钢筋计算

取ζ=1.3，则由公式（6-5）可得

取用箍筋直径为8，Ast1=50.3mm2，则

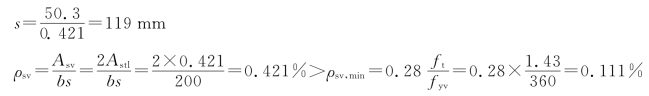
由公式（6-6）中ζ的定义可得

箍筋取8＠100，纵筋选用410，Astl=314mm2。

例题6-2 钢筋混凝土T 形截面纯扭构件的截面尺寸为（图6-7）：b=200mm，h=450mm，80mm，纵筋混凝土保护层厚度cs=30mm，承受扭矩设计值T=12.6kN·m。混凝土强度等级为C30，纵筋和箍筋均采用HRB400 级钢筋（fyv=360N／mm2），试计算其配筋。

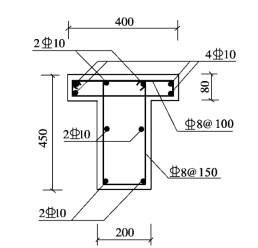
图6-7 例题6-2

解 （1）验算构件截面尺寸

（2）扭矩分配

对腹板

对上翼缘

（3）腹板配筋计算

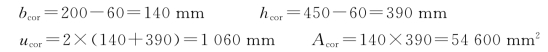
取ζ=1.1，则

取用箍筋直径为8，Astl=50.3mm2，则

箍筋间距取150mm，纵筋选用610，Astl=471mm2。

（4）上翼缘配筋计算

取ζ=1.3，则

取用箍筋直径为8，Astl=50.3mm2，则

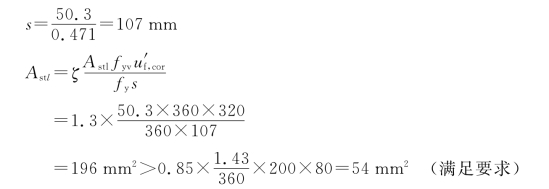
箍筋间距取100mm，纵筋选用410，Astl=314mm2。