混凝土结构与砌体结构的基本计算公式-第4版

1）计算应力图形

根据适筋截面在破坏瞬间的应力状态，并考虑第三章所述的计算原则，采用材料的强度设计值进行计算，则单筋矩形截面受弯承载力的计算应力图形如图4-12所示。这时，受拉区混凝土不承担拉力，全部拉力由钢筋承担，钢筋的拉应力达到其抗拉强度设计值fy，受压区混凝土应力图形简化为矩形，其应力值取为等效混凝土抗压强度设计值α1fc，受压区高度x 取为β1xa。

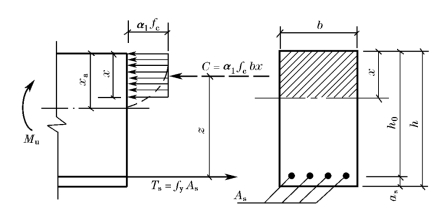
图4-12 单筋矩形截面受弯承载力计算应力图形

2）计算公式

按图4-12所示计算应力图形，单筋矩形截面构件正截面受弯承载力计算公式可根据力的平衡条件推导如下。

由截面上水平方向的内力之和为零，即∑X=0，可得

式中 fc——混凝土轴心抗压强度设计值；

b——截面宽度；

x——混凝土受压区高度；

fy——钢筋抗拉强度设计值；

As——纵向受拉钢筋截面面积。

公式（4-9）可改变为

式中 ξ——相对受压区高度（也可称为受压区高度系数）。

由截面上内、外力对受拉钢筋合力点的力矩之和等于零，即∑M=0，可得

式中 Mu——正截面受弯承载力设计值；

h0——截面的有效高度。

公式（4-10）可改写为

如果截面上内、外力的力矩平衡条件不是对受拉钢筋合力点取矩，而是对受压区混凝土合力点取矩，则得

或

(www.xing528.com)

3）适用条件

公式（4-10）和公式（4-11）仅适用于适筋截面，而不适用于超筋截面，因为超筋截面破坏时钢筋的拉应力σs 并未达到屈服强度，这时的钢筋应力σs 为未知数，故在以上公式中不能按fy 考虑，上述平衡条件不能成立。由4.3.3节可知，对于适筋截面应满足公式（4-8）或（4-8a）的条件。

由公式（4-9）可得于是，适用条件，即公式（4-8）可改写为

由此可得适筋截面的最大配筋率ρmax为

由公式（4-10）可得适筋截面的最大受弯承载力设计值为

即

令

则

于是，适用条件又可改写为

当混凝土强度不大于C50时，对于常用的钢筋品种，ξb 和αs，max可按表4-1采取。

表4-1 界限破坏时的相对受压区高度ξb 和αs，max

试验表明，超筋截面（截面实际配筋率ρ≥ρmax）的受弯承载力设计值基本上与配筋率无关，这时其受弯承载力设计值可按上述Mmax确定。

此外，设计截面时还应满足最小配筋率的要求，亦即应符合下列条件：

必须注意，验算纵向受拉钢筋最小配筋时，计算配筋率的截面面积应取全截面面积（b×h），不应取有效截面面积（b×h0），为区别起见，其配筋率用ρ1 表示。《规范》规定，对于矩形截面，最小配筋率ρ1min取0.2%和二者的较大值，详见附表15。