混凝土的变形-《混凝土结构与砌体结构第4版》

混凝土的变形可分为两类。一类是由于受力而产生的变形；另一类是由收缩和温湿度

变化而产生的变形。

1）混凝土在一次短期加荷时的变形性能

（1）混凝土的应力-应变曲线

混凝土的应力-应变关系是混凝土力学特性的一个重要方面，在钢筋混凝土结构承载力计算、变形验算、超静定结构内力重分布分析、结构延性计算和有限元非线性分析等方面，它都是理论分析的基本依据。

典型的混凝土应力-应变曲线包括上升段和下降段两部分（图2-5）。在上升段，当应力较小时，一般在（0.3～0.4以下时，混凝土可视为线弹性体，超过（0.3～0.4）时，应力-应变曲线逐渐弯曲（在图2-5中，εce为弹性应变，εcp为塑性应变）。当应力达到峰值点C 后，曲线开始下降。在下降段，曲线渐趋平缓，并有一个反弯点（D 点）。

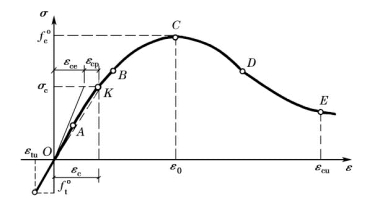
图2-5 混凝土应力-应变曲线

影响混凝土应力-应变曲线的因素很多，诸如混凝土的强度、组成材料的性质、配合比、龄期、试验方法以及箍筋约束等。试验表明，混凝土强度对其应力-应变曲线有一定的影响。如图2-6所示，对于上升段，混凝土强度的影响较小，与应力峰值点相应的应变大致为0.002，随着混凝土强度增大，则应力峰值点处的应变也稍大些。对于下降段，混凝土强度有较大的影响，混凝土强度愈高，应力下降愈剧烈，延性也就愈差。加荷速度也影响着混凝土应力-应变曲线的形状。图2-7所示为相同强度的混凝土在不同应变速度下的应力-应变曲线。由图中可见，应变速度愈大，下降段愈陡，反之，下降段要平缓些。

图2-6 不同强度混凝土的受压应力-应变曲线

图2-7 不同应变速度下的混凝土应力-应变曲线

（2）混凝土受压时纵向应变与横向应变的关系

在一次短期加压时，混凝土除了在纵向产生压缩应变外，还将在横向产生膨胀应变，横向应变与纵向应变的比值，称为横向变形系数，又称为泊松比νc。

在不同应力下，横向变形系数的变化如图2-8所示。当混凝土应力小于时，横向变形系数基本上保持为常数（《规范》中取νc=0.2）。当混凝土压应力超过时，横向变形系数逐渐增大，应力愈大，增大的速度愈快。

混凝土体积应变εv 与应力的关系如图2-9所示。当混凝土压应力较小时，体积随压应力增大而减小。然后，随压应力增大，体积又重新增大，最后，竟超过了原来的体积。

（3）混凝土的弹性模量、变形模量和剪变模量

在实际工程中，为了计算结构的变形、混凝土及钢筋的应力分布和预应力损失等，都必须要有一个材料常数——弹性模量。而混凝土的拉、压弹性模量与钢材不同，混凝土的拉、压应力与应变的比值不是常数，是随着混凝土的应力变化而变化。所以混凝土弹性模量的取值比钢材复杂得多。

混凝土的弹性模量有三种表示方法（图2-10）：

图2-8 混凝土横向变形系数与应力的关系

图2-9 混凝土体积应变与应力的关系

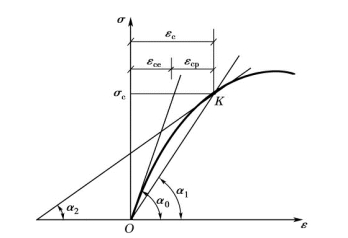
图2-10 混凝土的弹性模量、变形模和切线模量

①原点弹性模量

在混凝土受压应力-应变曲线的原点作切线，该切线的

斜率即为原点弹性模量（简称弹性模量），即

②变形模量

连接混凝土应力-应变曲线的原点O 及曲线上某一点K 作一割线，K 点混凝土应力为σc，则该割线（OK）的斜率即为变形模量，也称为割线模量或弹塑性模量，即

③切线模量

在混凝土应力-应变曲线上某一应力σc处作一切线，该切线的斜率即为相应于应力σc 时的切线模量，即

在某一应力σc 下，混凝土应变εc 可认为是由弹性应变εce和塑性应变εcp两部分组成。于是混凝土的变形模量与弹性模量的关系为

(www.xing528.com)

式中 ν——弹性特征系数，即ν=εce／εc。

弹性特征系数ν与应力值有关。当时，ν=0.8～0.9；当时，ν=0.4～0.8。一般情况下，混凝土强度愈高，ν值愈大。

对于混凝土弹性模量Ec，目前各国还没有统一的试验方法。显然，在混凝土一次加荷的应力-应变曲线上作原点的切线，以求得α0 的准确值是不容易的（由于试验结果很不稳定）。我国《规范》规定的弹性模量是按下述方法确定的：在试验的棱柱体上先加荷至，然后卸荷至零，再重复加荷、卸荷5次，并按应力为时的变形值计算其弹性模量。《普通混凝土力学性能试验方法》GBJ 81-85对上述试验方法略作修改，将加荷的应力改为，加荷、卸荷重复次数改为3次。由于混凝土不是弹性材料，每次卸荷至应力为零时，变形不能全部恢复，即存在残余变形。随着加荷、卸荷次数的增加，应力-应变曲线渐趋于稳定，并基本上接近直线。该直线的斜率即为混凝土的弹性模量。试验结果表明，按上述方法测得的弹性模量比按应力-应变曲线原点切线斜率确定的弹性模量要略低一些。

根据试验结果，《规范》规定，混凝土受压弹性模量按下列公式计算：

式中Ec 和fcu，k的计量单位为N／mm2。

混凝土的剪变模量可根据胡克定律，按下式确定：

式中 τ——剪应力；

γ——剪应变。

由于目前还没有适当的抗剪试验方法，要通过试验求得混凝土的剪变模量是困难的，所以混凝土的剪变模量Gc 一般可根据抗压试验测得的弹性模量Ec 和泊松比按下式确定：

在《规范》中取νc=0.2，故近似取Gc=0.4Ec。

2）混凝土在长期荷载作用下的变形性能

在荷载的长期作用下，混凝土的变形将随时间而增加，亦即在应力不变的情况下，混凝土的应变随时间继续增长，这种现象称为混凝土的徐变。徐变对钢筋混凝土和预应力混凝土结构有着有利和不利两方面的影响。在某些情况下，徐变有利于防止结构物产生裂缝，同时还有利于结构或构件内力重分布。但在预应力混凝土结构中，徐变则引起预应力损失。徐变变形还可能超过弹性变形，甚至达到弹性变形的2～4倍，因而能够改变超静定结构的应力状态，所以对混凝土徐变的试验研究已为大家所重视。

混凝土徐变与时间的关系如图2-11所示，在图中，t为时间，mon表示以月（month）为单位。图2-11是混凝土立方强度为40.3N／mm2 的100mm×100mm×400mm 棱柱体试件在相对湿度65%、温度20℃、承受的徐变试验曲线。从图2-11可见，24个月的徐变εcc约为加荷时立即产生的瞬时应变εci的2～4倍，前期徐变增长很快，6个月可达最终徐变的70%～80%，以后徐变增长逐渐缓慢。从图2-11还可看到，在卸荷后，应变会恢复一部分，其中立即恢复的一部分应变称为混凝土瞬时弹性回缩应变（εcir）；再经过一段时间（约20天）后才逐渐恢复的那部分应变称为弹性后效（εchr）；最后剩下的不可恢复的应变称为永久应变或塑性应变（εcp），即残余应变。

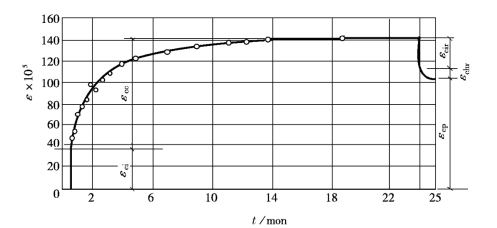
图2-11 混凝土的徐变

εci-加荷时瞬时应变； εcir-卸荷时瞬时弹性回缩应变；
εchr-卸荷后弹性后效； εcc-徐变； εcp-残余应变

影响混凝土徐变的因素很多，其主要规律如下：

（1）施加的初应力对混凝土徐变有重要影响（图2-12）。当压应力时，徐变大致与应力成正比，称为线性徐变。混凝土的徐变随着加荷时间的延长而逐渐增加，在加荷初期增加很快，以后逐渐减缓以致停止；当压应力时，徐变的增长较应力的增大为快，这种现象称为非线性徐变；应力过高（如）时的非线性徐变往往是不收敛的，从而导致混凝土的破坏。

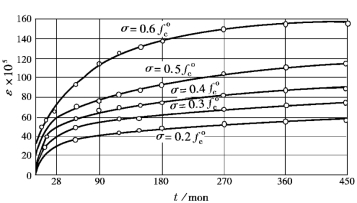
图2-12 混凝土徐变与初应力的关系

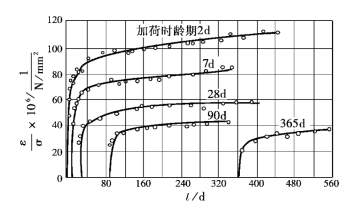
图2-13 混凝土徐变与加荷龄期的关系

（2）加荷龄期对徐变也有重要影响。加荷时的混凝土龄期越短，即混凝土越“年轻”，徐变越大（图2-13）。在图2-13中，t为龄期，d表示以天为单位。

（3）养护和使用条件下的温湿度是影响徐变的重要环境因素。受荷前养护的温度愈高，湿度愈大，水泥水化作用就愈充分，徐变就愈小。加荷期间温度愈高，湿度愈低，徐变就愈大。

（4）混凝土组成成分对徐变有很大影响。混凝土中水泥用量越多，或者水灰比越大，徐变越大。相同强度的水泥，徐变随所用水泥品种按下列顺序而增加：早强水泥，高强水泥，普通硅酸盐水泥，矿渣硅酸盐水泥。

（5）结构尺寸越小，徐变越大，所以增大试件横截面可减少徐变。混凝土中骨料强度和弹性模量越高，徐变越小。

3）混凝土在重复荷载作用下的变形性能

在重复荷载作用下混凝土的变形性能有着重要的变化。图2-14所示是混凝土受压棱柱体在一次加载、卸载时的应力-应变曲线。当混凝土棱柱体试件一次短期加载，其应力达到A 点时，试件加荷的应力-应变曲线为OA。这时，当全部卸载时，其卸载的应力-应变曲线为AC，它的瞬时应变恢复值为εcir；经过一段时间，其应变又恢复一部分，即弹性后效εchr；最后剩下永远不能恢复的应变，即残余应变εcp。

图2-14 混凝土一次加卸载的应力-应变曲线

图2-15所示为混凝土棱柱体在多次重复加载、卸载作用下的应力-应变曲线。由图2-15可见。随着重复荷载作用下应力值的不同，其应力-应变曲线也不相同。曲线①是一次连续加载时的应力-应变关系（上升段）；曲线②和③分别表示在压应力小于混凝土疲劳强度的应力σ1 和σ2 作用下，循环重复加载、卸载的应力-应变曲线。曲线②和③的特点是卸载和随后加载的应力-应变曲线都形成一封闭应力-应变滞回环，而且滞回环所包围的面积是随荷载重复次数的增加而逐渐减少的。这说明在重复荷载作用下，混凝土内部能量逐渐消失，混凝土内部组织结构渐趋稳定，直至卸载和随后的加载应力-应变曲线变成重合的直线。继续重复加载，混凝土的应力-应变关系仍保持线性关系，混凝土不会因混凝土内部开裂或变形过大而破坏。试验表明，这条直线与一次加载曲线在O 点的切线基本平行。在大于混凝土疲劳强度的应力σ3 作用下，循环重复加载、卸载时应力-应变曲线如曲线④所示，在循环重复加载、卸载初期，其变化情况和曲线②、③相似，但这只是暂时的稳定平衡现象，由于，每次加载会引起混凝土内部微裂缝不断发展，加载的应力-应变曲线会由凸向应力轴，逐渐变为凸向应变轴。随着荷载重复次数的增加，应力-应变曲线的斜率不断降低，最后因混凝土试件严重开裂或变形太大而破坏。这种因荷载重复作用而引起的混凝土破坏称为混凝土疲劳破坏。

图2-15 混凝土多次加载、卸载的应力-应变曲线