NSL的第一个最简单应用,就是确定在任意情况下汽车上的轴载荷。这是分析驱动(加速)性能的重要的第一步,因为轴载荷决定每个轴上可获得的驱动力,影响着加速度、爬坡能力、最大车辆速度,以及牵引车的挂钩力。如图2-61所示,该图中显示了大多数明显的力。
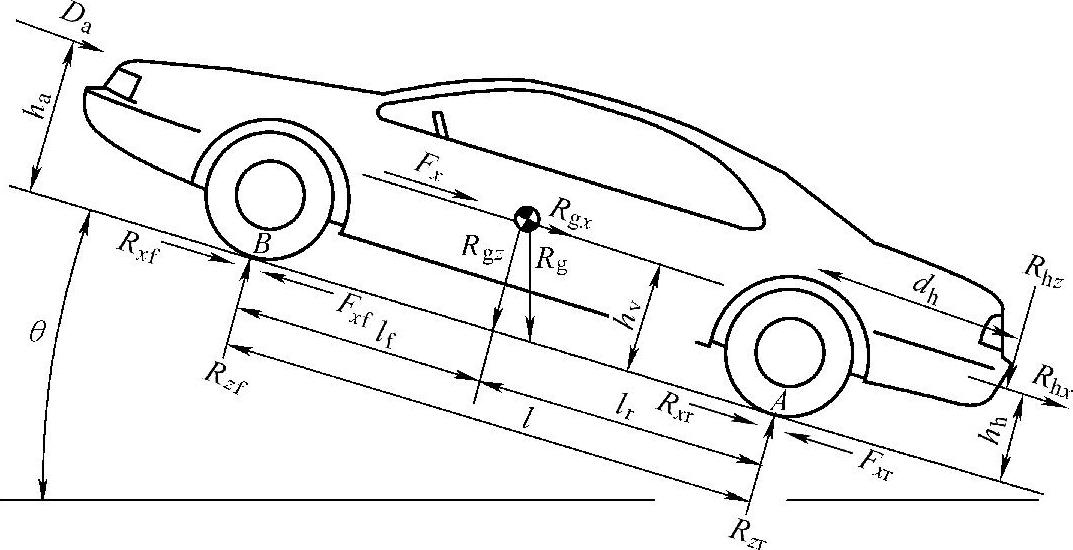
图2-61 作用在一辆汽车上的任意力【GILLESPIE 1992】
每根轴所带载荷可以包括一个静态部件,加上由其他作用在车辆上的力而引起的从前向后(或反过来)转移过来的载荷。前轴上的载荷可以通过对后车轮下的转矩求和而找到。假设车辆没有在加速,则A点的转矩总和必须为零。按照SAE约定,A点的顺时针转矩是正的,于是
Fzfl+Daha+Fxhv+Rhxhh+Rhzdh+Rgsinθhv-Rgcosθlr=0 (2.3)
或
mvfgl+Daha+mvaxhv+Rhxhh+Rhzdh+mvgsinθhv-mvgcosθlr=0 (2.4)
按照SAE约定,B点的顺时针转矩也是正的,于是:
Fzrl-Daha-Fxhv-Rhxhh-Rhz(dh+l)-Rgsinθhv-Rgcosθlf=0 (2.5)
或
mvrgl-Daha-mvaxhv-Rhxhh-Rhz(dh+l)-mvgsinθhv-mvgcosθlf=0 (2.6)
其中,Rg=mvg:重力,是车身受到地球吸引并作用在车身重心上的力,在斜坡上,该力可能有两个分量,即与垂直于公路/越野路面的余弦分量Rgz,以及平行于公路/越野路面的由斜坡引起的正弦分量Rgx(N);mv为作用在其重心的汽车的质量(kg);g为重力加速度(m/s2);Rgx=Rgsinθ,为在x轴方向由斜坡引起的在汽车上的附加力(N);Rgz=Rgcosθ,为在z轴方向由斜坡引起的在汽车上的附加力(N);θ为上坡/下坡坡度(rad);Fzf=mvfg,为作用在前轮轮胎z轴方向的垂直于公路/越野路面的动力(N);mvf为前轮所带载荷(kg);Fzr=mvrg,为作用在后轮轮胎z轴方向的垂直于公路/越野路面的动力(N);mvr为后轮所带载荷(kg);Fx=mvax,为当汽车沿公路/越野路面加速时,作用在重心的与加速度方向感相反的等效惯性力(N);Fxf=mvfax,为作用在前轮轮胎接地面地平面上的驱动力(N);Fxr=mvrax,为作用在后轮轮胎接地面地平面上的反作用力(驱动力)(N);ax为x轴方向的加速度(m/s2);Rxf为作用在前轮轮胎接地面地平面上的滚动阻力(N);Rxr为作用在后轮轮胎接地面地平面上的滚动阻力(N);Da为作用在车身的气动力;它可以表示为作用在地面上由高度ha(m)表示的某点的力,或者通过一个在地平面上的与空气动力俯仰力矩有关的同样大小的纵向力(N);Rhx为当车辆正拖引拖车时作用在连接点的纵向力(N);Rhz为当车辆正拖引拖车时作用在连接点的垂直力(N)。(https://www.xing528.com)
请注意,上坡姿势相当于一个正的θ角,这样正弦项为正;下坡姿势产生一个负的正弦项。
从式(2.3)~式(2.6),可以算出Fzr和Fzr,以及mvf和mvr。
于是,轴载荷各自的表达式为
Fzf=(Rgcosθlr-Daha-Fxhv-Rhxhh-Rhzdh-Rgsinθhv)/l (2.7)
及
Fzr=[(Rgcosθlf+Daha+Fxhv+Rhxhh+Rhz(dh+l)+Rgsinθhv)]/l (2.8)
或
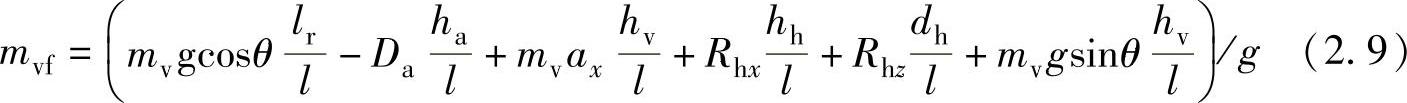
和
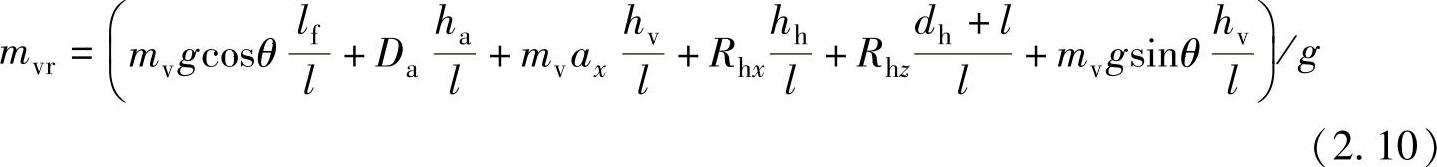
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




