车地间毫米波通信技术在轨道交通中的能量效率分析

为进一步分析全双工大规模MIMO 系统的性能，本小节将重点研究全双工大规模MIMO 系统的能量效率。能量效率可以定义为[107]

其中， Pmix、 Pfilt、 Psyn、 PLNA、 PIFA、 Pfilr、 PAGC、 PDAC和 PADC分别表示混频器，发射机侧的有源滤波器、频率合成器、低噪声放大器、中频放大器，接收机侧的有源滤波器、自动增益控制、低精度 ADC 和低精度DAC 的功率消耗[123]。此外， cA和 cD是与ADC 和DAC 精度有关的标志[127]，其取值如下：

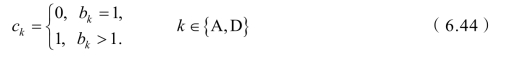
对 ADC 和 DAC 的硬件功耗分别进行建模，并且其数值取决于ADC/DAC 量化位数，则具体模型可以表示为[128]

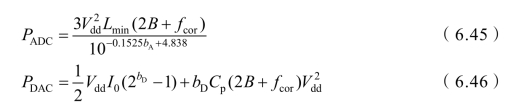
其中， bA和 bD分别表示ADC 和DAC 的量化位数； Vdd是转换器的电源；I0表示对应于最低有效位的单位电流源； Cp表示转换器中每个开关的寄生电容； Lmin表示给定CMOS 技术的最小通道长度； fcor是1/ f 噪声的转折频率[128]。

对低精度ADCs/DACs 架构下的全双工大规模MIMO 系统的频谱效率和能量效率解析结果进行仿真验证，具体的参数设置如表 6.2 所示[122，123，127]。对于所有的仿真，大尺度衰落均建模为βa，n=za，n/(da，n/ rd) -v，其中a∈(U，D)表示全双工大规模MIMO 系统上行链路或下行链路。这里针对采用不同基站天线数、用户发送功率、莱斯因子、ADC/DAC 的量化精度、回路干扰程度和残余回路干扰功率等，对频谱效率和能量效率进行仿真分析与研究。

表6.2　仿真参数设置

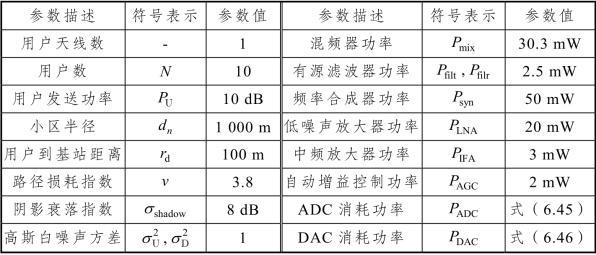
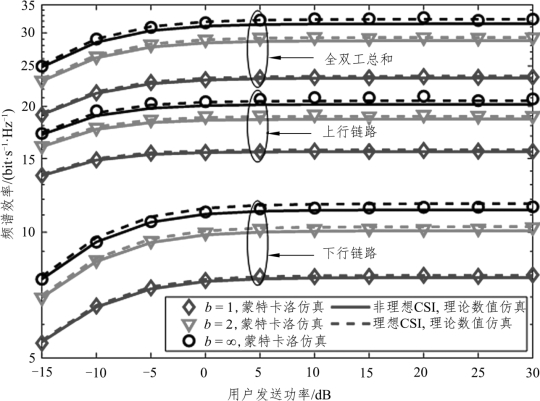
图6.2　不同ADC/DAC 量化精度下的用户发送功率和频谱效率的关系

图6.2 给出了不同ADC/DAC 量化精度的情况下，频谱效率与用户发送功率的关系。仿真中固定设置用户数N = 10，基站天线数M =100，CSI误差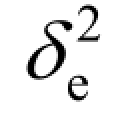 =0.001，莱斯因子KU，n=KD，n=Kn= 6dB，基站发送功率PD=10PU和ADC/DAC 量化精度 bA=bD= b。由图6.2 可知，理论分析和蒙特卡洛仿真曲线都非常紧凑，这说明上述推导结果是完全正确的。同时，随着用户发送功率的增加，各组频谱效率曲线不断增加并逐渐接近上界值，这与式（6.24）和式（6.37）的理论分析结果完全一致，这意味着全双工大规模MIMO 系统不能仅通过增加用户/基站发送功率来无限提升系统的频谱效率。此外，当用户发送功率较小（PU＜5dB）时，理想CSI 系统频谱效率性能优于非理想CSI 系统；当用户发送功率进一步增大时，CSI误差对系统性能的影响减小。

图6.3 给出了理想CSI 和不同基站天线数的情况下，频谱效率与莱斯因子的关系。仿真中固定设置用户数N = 10，用户发送功率PU=10dB，基站发送功率PD=10PU和ADC/DAC 量化精度 bA= bD= 2bit。由图6.3 可知，理论分析与蒙特卡洛仿真结果在M ={50，150，250，350}这四种情况下都十分吻合。同时，当莱斯因子趋于无穷大时，全双工系统总频谱效率趋近于一个常数，这与式（6.21）和式（6.34）的理论分析结果一致。这意味着在莱斯信道场景下，适当地增大莱斯因子可以促进频谱效率得到提升，但是当莱斯因子逐渐增大并趋于无穷大时，并不能无限提升系统的性能。

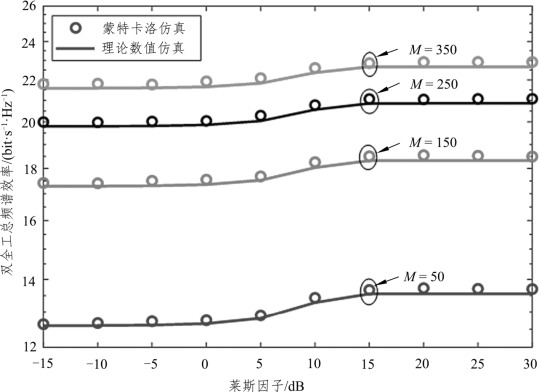
图6.3　不同基站天线数下的莱斯因子和频谱效率的关系

图6.4 给出了不同信道场景和ADC/DAC 量化精度的情况下，频谱效率和基站收/发天线数的关系。仿真中固定设置用户数N = 10，用户发送功率PU=10dB，基站发送功率PD=10PU和莱斯因子KU，n=KD，n= 6dB。由图6.4 可知，图中提供了4 种不同信道场景下的频谱效率进行比较，分别为：① 半双工瑞利信道场景；② 全双工瑞利信道场景；③ 半双工莱斯信道场景；④ 全双工莱斯信道场景。从中可以看出，随着基站收/发天线数的增加，各组频谱效率曲线具有相似的增长曲线。同时，图中清晰地表明，全双工模式下的性能明显优于半双工模式。此外，对于较低的ADC/DAC 精度，莱斯信道场景下的系统频谱效率优于瑞利信道场景下的频谱效率，而对于理想的ADC/DAC，其频谱效率差距减小。由此可知，在增加基站天线和ADC/DAC 精度的前提下，全双工模式的工作效率总体上优于半双工模式，并且这种优势随着基站天线和ADC/DAC 精度的增加而更加显著。(www.xing528.com)

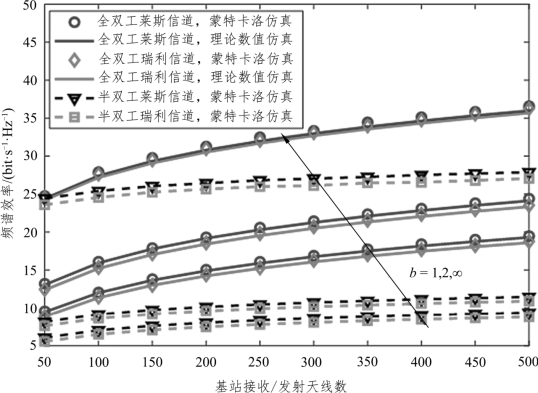
图6.4　不同信道场景和ADC/DAC 量化精度下的基站天线数和频谱效率的关系

图6.5 给出了不同基站天线数的情况下，ADC/DAC 量化位数和频谱效率的关系。仿真中固定设置用户数N = 10，莱斯因子KU，n=KD，n= 6dB，用户发送功率PU=10dB，基站发送功率PD=10PU和ADC/DAC 量化精度bA=bD= b。图6.5 中提供了频谱效率的蒙特卡洛仿真和理论分析值（包括上行链路，下行链路和全双工总和）。从图中可以看出，随着ADC/DAC量化精度的提高，各组曲线都具有相似的增长趋势。同时当 ADC/DAC量化位数从1 位增加到3 位时，各组频谱效率曲线得到快速增长趋势。但是，随着ADC/DAC 量化精度的进一步提高，各组频谱效率曲线将缓慢增长并逐渐达到极限，这与式（6.23）和式（6.36）的理论分析结果一致。此外，在低精度ADC/DAC 量化位数从1 位变为10 位的过程中，随着基站天线数的进一步增加，系统的频谱效率将得到显著地提升。

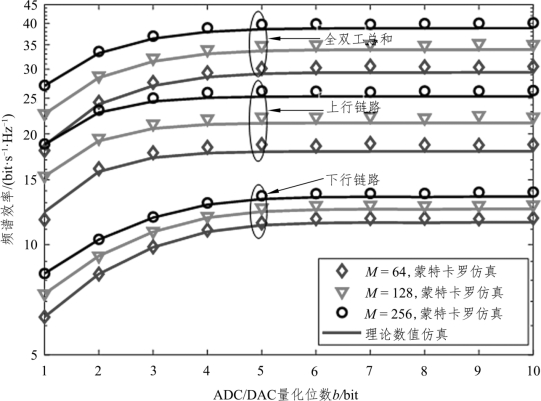
图6.5　不同基站天线数下的ADC/DAC 量化位数和频谱效率的关系

图6.6 给出了不同工作模式的情况下，频谱效率和残余回路干扰功率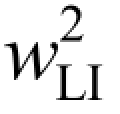 的关系。仿真中固定设置用户数N = 10，莱斯因子Kn= 6dB，用户发送功率PU=10dB，基站发送功率PD=10PU和 ADC/DAC 量化精度bA=bD= b。由图6.6 可知，当使用2 bit 的ADC/DAC 时，全双工工作模式下的大规模 MIMO 系统的性能会随着残余回路干扰功率的增加而降低。在残余回路干扰功率较低时，全双工模式下的系统频谱效率性能优于半双工模式。对于较大的残余回路干扰功率，半双工模式的性能更好。此外，在基站部署更多的天线可以减轻残余回路干扰功率的影响，尤其是将基站天线数从100 增加到500，可以大大提高全双工系统的性能。

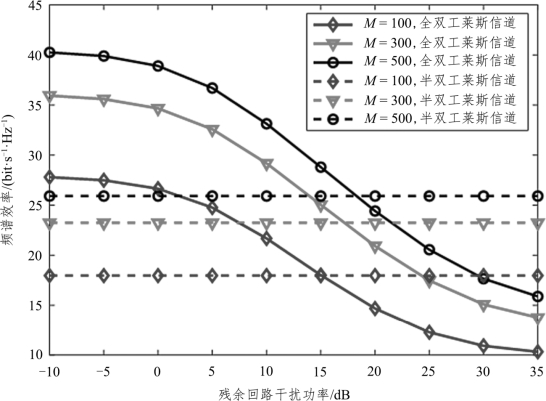
图6.6　不同基站天线数和工作模式下的残余回路干扰功率和
频谱效率的关系

图 6.7 给出了不同基站天线数和 CSI 的情况下，能量效率和ADC/DAC 量化精度的关系。仿真中固定设置用户数N = 10，CSI 误差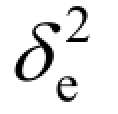=0.001，莱斯因子KU，n=KD，n=Kn= 6 dB，用户发送功率PU=10 dB，基站发送功率PD=10PU和ADC/DAC 量化精度 bA=bD= b。从图6.7 可知，随着ADC/DAC 精度的提高，能量效率曲线先升后降，期间出现峰值。这是由于b=1 ～3bit 的ADC/DAC 功耗较低，因此能够快速提升系统能量效率；当b ＞ 3bit 后，随着量化精度进一步提高，ADC/DAC 的功耗急剧增加，因此呈现能量效率逐渐下降的趋势。同时，随着基站天线数的增加，能量效率反而更低，这是由于更多的基站天线意味着要部署同等数量的ADC/DAC 接收机，也会加剧回路间的相互干扰，综合各项因素，导致能量效率降低。此外，非理想CSI 下系统能量效率略低于理想CSI 下系统。

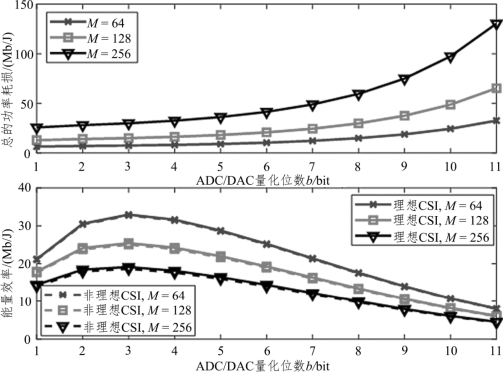
图6.7　不同基站天线数下的ADC/DAC 量化精度和频谱效率的关系

图6.8 给出了不同基站天线数和莱斯因子的情况下，系统总的功率损耗和频谱效率之间的权衡关系。仿真中固定设置用户数N = 10，用户发送功率PU=10dB ， 基站发送功率PD=10PU和 ADC/DAC 量化精度bA=bD= b。通过将ADC/DAC 量化位数从1 bit（对应于每条曲线的左下端）调整到10 bit（对应于每条曲线的右端）来获得各组曲线。由图6.8可知，当ADC/DAC 量化位数从1 bit 增加到3 bit 时，可以快速提升全双工大规模MIMO 系统的频谱效率。对于更高的量化精度，由于功率损耗占主导地位，相对精度的提高，频谱效率的增加趋势大大降低。此外，在相同的功耗下，可以通过增加基站天线数来提高频谱效率。同时，具有较大莱斯因子的系统具有更好的性能。

图6.9 给出了不同基站天线数和莱斯因子的情况下，能量效率和频谱效率之间的权衡分析。仿真中固定设置用户数N = 10，用户发送功率PU=10dB，基站发送功率PD=10PU和ADC/DAC 量化精度 bA=bD= b。由图6.9 可知，具有较大莱斯因子的曲线包含的区域面积更大，这意味着具有较大莱斯因子的系统拥有更好的性能。同时，可以看出，当量化位数较小（如1 ～ 3bit）时，频谱效率的轻微降低可以使能量效率得到大幅度的提升。但是，当量化位数较大时，能量效率随着量化位数进一步增加而逐渐呈现下降趋势。此外，增加基站天线数可以显著改善系统的整体性能。例如，M = 64和M =256两种情况，尽管后者的能量效率略低，但是频谱效率却得到了显著提高。因此，为了在能量效率和频谱效率之间进行折中，增加基站天线数会导致频谱效率的增益高于能量效率的增益。

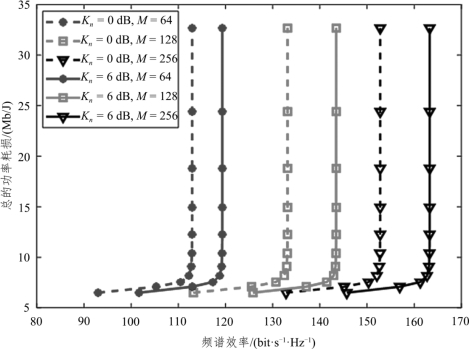
图6.8　不同基站天线数和莱斯因子下的总的功率损耗和频谱效率之间的权衡

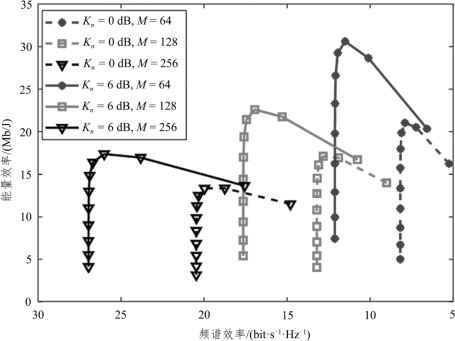
图6.9　不同基站天线数和莱斯因子下的能量效率和频谱效率之间的权衡