【摘要】：为了便于分析，采用加性量化噪声模型对ADC 量化误差和DAC 失真进行建模[122，124]。然后，经过ADC 量化处理后的基站接收信号可以表示为其中，qU～CN是与 yU不相关的加性高斯量化噪声； αu= 1- ρu为线性量化增益，其值取决于ADC 量化位数 bA。表6.1不同ADC/DAC 量化位数 bA下 ρu( ρd)的近似值对于固定信道 GD，GU和 GLI， qD和 qU的协方差矩阵可以表示为证明：由于RqU的推导需要下行链路信号统计结果，因此先处理下行链路信号，并推导出式。
为了便于分析，采用加性量化噪声模型对ADC 量化误差和DAC 失真进行建模[122，124]。然后，经过ADC 量化处理后的基站接收信号可以表示为
其中，qU～CN(0，RqU)是与 yU不相关的加性高斯量化噪声； αu= 1- ρu为线性量化增益，其值取决于ADC 量化位数 bA。如果给定 bA，则 αu值可以在表6.1 中获得。
经过DAC 处理后，下行用户的接收信号 yD可以表示为
其中，qD～CN(0，RqD)是与 yD不相关的加性高斯量化噪声； αd= 1- ρd为线性量化增益，其值取决于DAC 量化位数 bA[125]。同样，如果给定 bD，则 αd值可以在表6.1 中获得。
表6.1 不同ADC/DAC 量化位数 bA (bD)下 ρu( ρd)的近似值
对于固定信道 GD，GU和 GLI， qD和 qU的协方差矩阵可以表示为
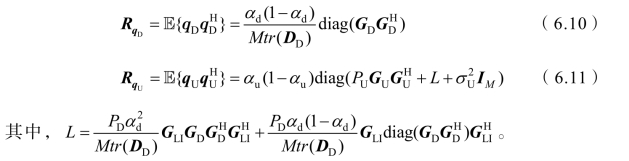(www.xing528.com)
证明：由于RqU的推导需要下行链路信号统计结果，因此先处理下行链路信号，并推导出式（6.10）。由式（6.6）可知，对于第m 个天线/维度，有
对于上行链路的处理方法相似，则有
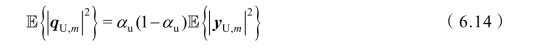
将式（6.6）和式（6.9）代入式（6.5）中，则有
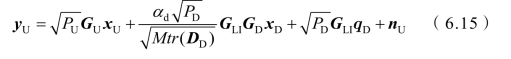
由式（6.15）可得
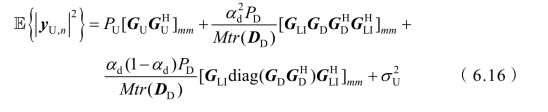
因此，将式（6.16）代入式（6.14），且 E {qU，m}=0，则式（6.11）证毕。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
