地间毫米波通信技术在混合精度ADC接收机下的频谱效率分析

本小节主要研究空间相关信道下，混合精度 ADC 架构的大规模MIMO 上行系统性能。由式（5.9）中的信号经过最大比合并r =F Hy 后，则理想CSI 条件下基站端接收到的信号为

由式（5.27）可知，理想CSI 条件下第k 个用户的输出信号kr 表示为

其中， f0，k和 f1，k为信道矩阵 F0和 F1的第k 列元素。式（5.28）右边首项为用户k 发送的信号，其余三项分别为来自其他用户干扰信号、信道噪声和量化噪声。

由式（5.28）可知，理想CSI 条件下第k 个用户在大规模MIMO 上行系统的频谱效率可以表示为

定理5.3：在空间相关信道场景下，对于混合精度ADC 架构的多用户大规模MIMO 上行系统，若基站端采用MRC 检测算法处理信号，则理想CSI 下第k 个用户在大规模MIMO 上行系统的频谱效率可以近似为

证明：在理想CSI 条件下，对于具有庞大天线数量的混合精度ADC架构大规模MIMO 上行系统，仍采用定理5.1 中方法，求取频谱效率的近似表达式，则式（5.29）可以进一步表示为

其中，步骤(ζ )成立的条件为：对于∀m= 1， …，M ，假设[ R]mm=1，则可得式（5.35）。然后，将式（5.32）、式（5.33）、式（5.34）和式（5.35）代入式（5.31）并进行化简，即可得到式（5.30），证毕。

为便于全面理解定理5.3，下面给出一些具有特殊取值的系统参数来分析上行链路频谱效率性能，如用户发送功率、空间相关系数、基站天线数和低精度ADC 量化位数等。针对给出的参数设置，下面将讨论几个特殊场景下的近似结果。

（1）固定基站天线数M 、空间相关系数η 和ADC 量化位数b 不变，当用户发送功率 pu→∞时，则式（5.30）的频谱效率可以简化为

由式（5.36）可知，频谱效率增加过程中将会出现饱和效应。当用户发送功率趋于无穷大时，频谱效率数值将取决于低精度ADC 量化位数和空间相关系数。同时，随着用户平均发送功率的逐渐增加，混合精度ADC架构的大规模MIMO 上行系统频谱效率并不会无限提高。

（2）在不相关的大规模MIMO 信道下（即η =0 ），固定基站天线数M 、用户发送功率 pu和低精度ADC 量化位数b 不变，则式（5.30）的频谱效率可以简化为

其中，v =M0+α2M1。由式（5.37）和式（5.30）可知，当空间相关系数η = 0时，本章的空间相关信道模型退化为一般的瑞利衰落信道模型。同时，式（5.37）的频谱效率结果与文献[114]中式（15）的结果一致。(www.xing528.com)

同理，非理想CSI 条件下，基站端经过最大比合并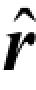 = 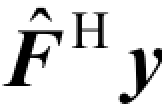处理后，则第k 个用户的输出信号可以表示为

其中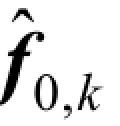， 和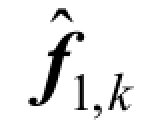分别为信道矩阵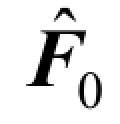和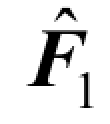的第k 列元素。式（5.38）右边首项为用户k 发送的信号，其余四项分别为用户干扰信号、信道估计误差信号、信道噪声和量化噪声。

由式（5.38）可知，非理想 CSI 条件下第k 个用户在大规模MIMO上行系统的频谱效率可以表示为

定理5.4 在空间相关信道场景下，对于混合精度ADC 架构的多用户大规模MIMO 上行系统，若基站端采用MRC 检测算法处理信号，则非理想CSI 下第k 个用户在大规模MIMO 上行系统的频谱效率可以近似为

证明 在非理想 CSI 条件下，对于具有大型天线阵列的混合精度ADC 架构大规模MIMO 系统，采用与定理5.4 相似的方法，则式（5.39）可以近似表示为

对于式（5.41）分母最后一项的计算，采用式（5.35）相同的求解方法，则

然后，将式（5.42）～式（5.46）代入式（5.41）并经过化简，即可得到式（5.40）。

证毕。

由式（5.30）和式（5.40）可知，小区总的频谱效率可以定义为所有用户的频谱效率之和，则

其中，Ω ∈{P ，IP}表示理想或非理想CSI 下混合精度ADC 架构的大规模MIMO 上行系统；RΩ，sum表示小区近似频谱效率；RΩ，k表示用户k 的近似频谱效率。