低精度ADC信道模型

考虑一个存在干扰机的单小区多用户大规模MIMO 上行系统，如图5.1 所示。假设该系统基站端配备 M (M≫ K≥ 2)根接收天线；用户端有K个单天线用户和一个单天线干扰机组成，并且用户之间相互独立。

根据Kronecker 相关模型[106，107]，则理想CSI 条件下的空间相关信道模型建模为

其中，R ∈CM×M为信道相关矩阵；H ∈CM×M为小尺度衰落系数矩阵，其元素是服从零均值和单位方差的复高斯随机变量；而D 是K × K的实对角矩阵，其对角线上的元素[ D]kk=βk为第k 个用户到基站的大尺度衰落系数，包括路径损耗和阴影衰落，即

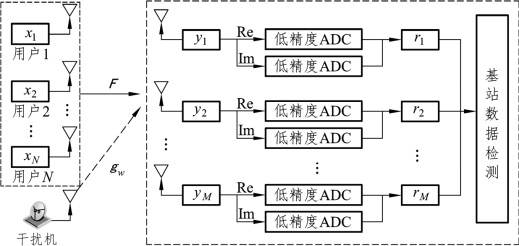
图5.1　干扰机和低精度ADC 架构下大规模MIMO 系统框图

其中， zk是标准差为 σshadow的对数正态随机变量，并表示阴影衰落。 dk为第k 个用户到基站的距离， rd为小区覆盖区域半径，v 为路径损耗指数。

根据Toeplitz 相关模型[108，109]，则R 的第( m， n )个元素可以表示为(www.xing528.com)

其中，上标*表示共轭运算，η 是基站接收天线间的相关系数，即0≤η ≤1 。显然，η = 0表示相邻天线之间空间不相关；η = 1表示相邻天线之间空间全相关。

基站端接收到的模拟信号y ∈CM×1可以表示为[112]

其中， pu为用户信号发送功率； qu为干扰机的信号发送功率；F ∈CM×K为用户到基站的信道矩阵；gw～CN(0，βwIM)为干扰机到基站的信道矩阵， βw为干扰机的大尺度衰落系数[113]；x ∈C K×1为用户发送的信号，且满足E{xxH}=IK， s 为干扰机发送的信号， 且满足E{ ssH} =1；n～CN(0，σ2IM)为复加性高斯白噪声，其中IA(A ∈{K ， M})表示A × A阶单位矩阵。随后采用AQNM 对接收到的信号进行量化处理yq=Q( y)，则经过低精度ADC 量化后的输出信号可以近似为