离散混合预编码设计在轨道交通车地间毫米波通信技术中的应用

混合预编码结构受益于大规模天线阵列和射频链路。假设发送的符号满足高斯分布，用户端完全解码且信道状态信息是已知的，在毫米波大规模MIMO 系统中，混合预编码部分连接结构中的系统频谱效率为

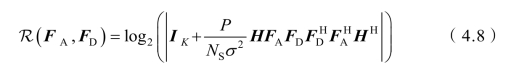
数据流在传输时，数字预编码 FD可以改变发射信号的幅度与相位，而模拟预编码 FA只改变信号的相位。移相器经过量化，矩阵 FA中的每个元素都属于集合U ，其中U 为

其中，Δ=2 π2B为均匀量化的补偿因子，B 为移相器的量化精度。 FA的约束条件为

其中，υ =e jΔ。通过使用离散移相器且在基站总功率约束下，混合预编码设计问题为

由于式（4.11）的约束条件的非凸特性，并且需要联合优化数字预编码与模拟预编码，直接对式（4.11）最优问题求解具有较大难度。在模拟预编码设计过程中，暂时不考虑移相器的量化影响，去除式（4.10）的约束限制。混合预编码设计问题可以转化为

其中，Gopt为最佳全数字预编码；At为ULA 或UPA 的阵列响应矢量。定义信道矩阵H 的奇异值分解为H =U ∑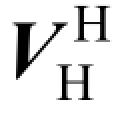 ，其中U 为酉矩阵，∑为元素值递减的对角矩阵，VH∈CK×M为右奇异向量。将VH分解为VH=[VH1VH2]，其中，VH1∈CK×NS。最佳全数字预编码为信道矩阵的奇异值分解后的右奇异向量的第NS列，可以得到全数字预编码Gopt=VH1。

对经过相应的天线响应矢量得出的模拟预编码进行量化，定义量化函数

其中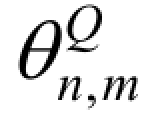，为θn，m的量化值； Q (·)表示量化运算，作用是将输入的值量化为集合U 中最近的点。 bs被选择的条件为

在式（4.12）的优化问题中，将模拟预编码矩阵 FA的约束条件及量化后的值代入式（4.12）中，其等价问题可以转化为[52]

因此，最佳模拟预编码矩阵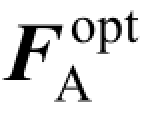与最佳数字预编码矩阵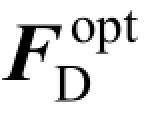可以通过式（4.12）与（4.15）获得。本节提出的离散化的正交匹配追踪算法的流程图如图4.2 所示。

算法的具体实现步骤：

步骤1：初始化模拟预编码矩阵 FA为全0 矩阵；

步骤3：外循环开始，n＝1；

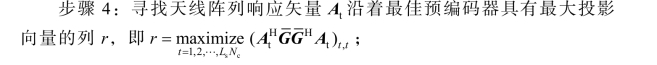
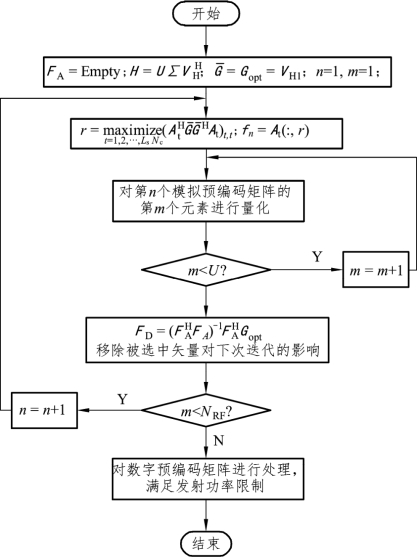
图4.2　离散化正交匹配追踪算法流程图

步骤5：将所选择天线阵列响应矢量的第r 列赋值于第n 个子模拟预编码矩阵；

步骤6：内循环开始，m＝1；(www.xing528.com)

经过步骤1 至步骤12 后，利用离散化的正交匹配追踪算法可以求出最终的最佳数字预编码器与最佳离散化的模拟预编码器。

为了验证所提出的离散混合预编码对系统性能的影响，仿真条件设置如表4.1 所示。

表4.1　系统参数设置

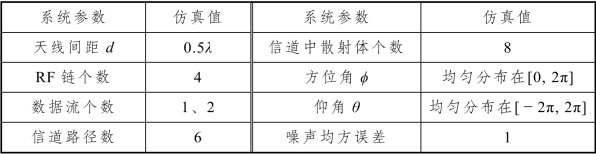
同时，为了验证所提出的离散化混合预编码方案的有效性，将通过Matlab 进行仿真分析所提出方案的有效性。在单用户大规模MIMO 场景中，分别考虑基站与用户配置两种天线阵列。一种为基站配置144 个ULA天线，用户端配置36 个ULA 天线；另一种为基站配置M = 12 × 12个天线的UPA，用户端配置M = 6 × 6个天线的UPA。假设所有信道增益符合高斯独立同分布。系统参数如表4.1 所示。

图4.3 为天线阵列为UPA 时，在输入不同SNR 的情况下，对比分析不同数据流中不同量化位数的混合预编码的频谱效率。由图4.3 可以观察出，增加数据流的传输量时，可以明显增加系统的频谱效率。同时，在相同的数据流NS的情况下，所提出的离散化混合预编码方案的频谱效率随着模拟预编码的量化位数B 的增加而增大，且在量化位数B=3 时，近乎达到未经过量化的混合预编码方案。这表明，所设计的离散化混合预编码方案更具有实用性。图4.3 中仿真结果验证了所提出的离散化混合预编码方案的有效性。低精度的模拟预编码器具有较好的性能，这得益于离散化混合预编码方案在每次迭代中降低了模拟预编码器量化过程中的性能损失，使得经过量化的模拟预编码器在每次迭代中得以一定补偿。

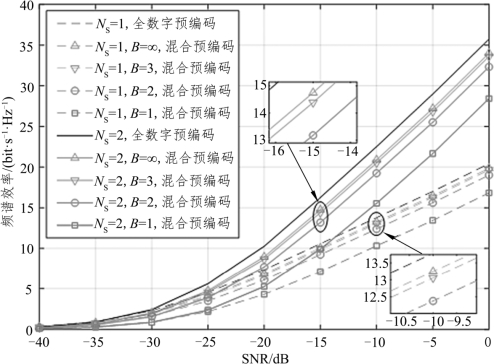
图4.3　不同数据流下频谱效率随SNR 变化情况

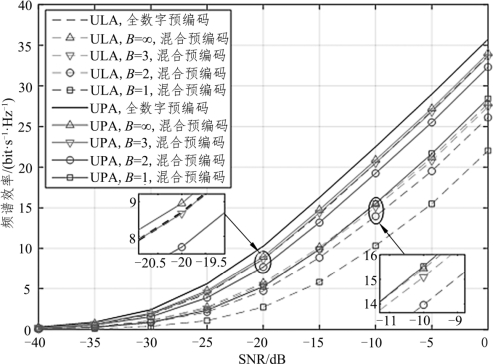
图4.4　不同天线阵列下频谱效率随SNR 变化情况

图4.4 所示为数据流NS=2 时，在输入不同SNR 的情况下，对比分析相同天线个数和间距的ULA 与UPA 不同量化位数的混合预编码的频谱效率。在相同情况下，UPA 的频谱效率优于ULA，且随着量化位数的增加，ULA 与UPA 的频谱效率均增加；考虑配置不同的天线阵列时，量化位数B=1 的UPA 的频谱效率接近未经过量化的ULA 的频谱效率。这些表明UPA 的天线性能增益明显优于ULA，造成该结果的原因是UPA的排列方式相对于ULA 较为集中，天线阵列响应矢量在进行方位角的调整中，基站端的UPA 发射的信号波束相对于ULA 更为集中，系统性能增益更优。

图4.5 为基站与用户端配置的天线为ULA，SNR =5 dB，且所传输的数据流NS=2 的情况下，系统频谱效率随着天线数量的变化情况。从图4.5 中可以观察到，随着天线数量的增加，不同量化位数的离散化预编码的频谱效率都逐渐增加；天线数量较少时，量化位数B=3 的离散化混合预编码方案的频谱效率接近于全数字预编码的频谱效率。这说明系统的性能增益可以通过增加天线数量来实现。同时，在较少天线数量时，较高量化值的混合预编码效果更接近全数字预编码的性能增益。

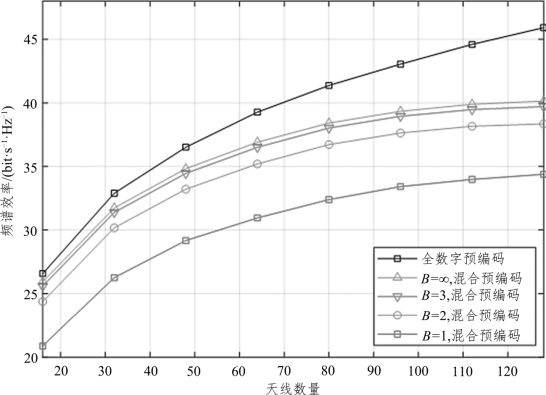
图4.5　系统频谱效率随天线数量的变化情况

图4.6 是基站与用户端配置的天线为ULA，SNR =0 dB，所传输的数据流NS=2 的情况下，系统频谱效率随着基站RF 链数量的变化情况。从图4.6 中可以看出，当RF 链的数量小于10 时，随着RF 链的数量逐渐增加，不同量化位数的离散化预编码的频谱效率都逐渐增加，且量化位数B=3 时的离散化混合预编码的频谱效率逐渐接近全数字预编码；当RF链的数量大于10 时，不同量化位数的离散化混合预编码几乎不变。这表明，在混合预编码过程中增加少量的RF 链可以提高系统的频谱效率，超过一定数量的RF 链不会提高系统的频谱效率。同时，在相同的RF 链的情况下，模拟预编码的量化位数越高时，系统的频谱效率越大，但总是小于全数字预编码方案的频谱效率。造成该部分的原因为：当RF 链数量增加到一定数量后，RF 链数量不是制约系统性能的主要因素，其他系统参数（如天线数量、数据流等）会进一步影响系统的性能，如需系统性能的进一步提高，则需要调整系统的其他参数。

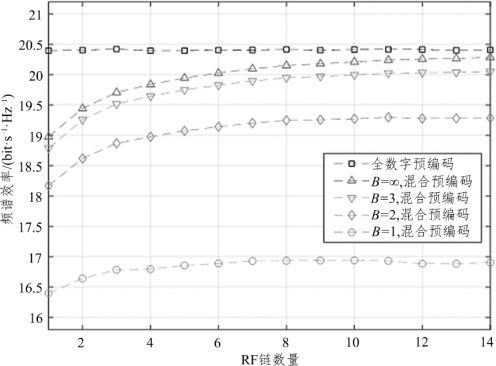
图4.6　系统频谱效率随RF 链数量的变化情况

图4.7 展示了在不同的数据流的情况下，系统频谱效率随移相器的量化精度的变化情况。从图4.7 可以看出，对于三种数据流，随着移相器的量化精度的逐渐增加，系统的频谱效率都先逐渐增加，不断接近于全数字的频谱效率，最后保持不变。当移相器的精度在低位时（b＜5），模拟预编码器对不同精度的移相器较为敏感，其精度越高，越接近于最佳的无限制的模拟预编码器。然而，当精度增加到一定精度后（b＞5），系统的模拟预编码矩阵已经接近或达到最优状态，系统的频谱效率不再随着量化精度的增加而增大。从图4.7 中可以看出，增加系统所需传输的数据流时，可以显著提高系统的频谱效率，且数据流越多时，其离散混合预编码的频谱效率越低于全数字预编码。

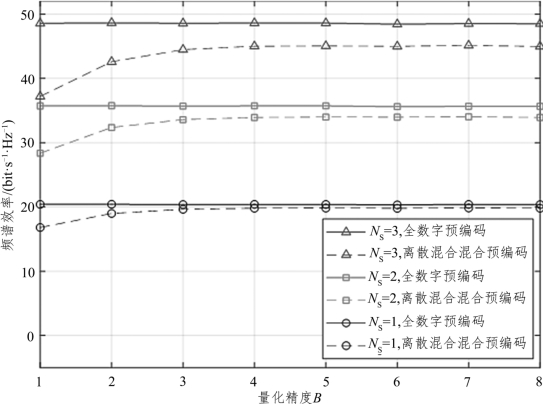
图4.7　系统频谱效率随移相器的量化精度的变化情况

考虑整个系统的能耗为 Ptot= Pt+NRFPRF+MPPS，其中， Pt=1 W为发射信号需要的能量， PRF=250 mW为RF 链消耗的能量， PPS为模拟预编码器端的移相器消耗的能量，M 为移相器的数目。当移相器精度为n 位时，其能量消耗与精度之间的关系为 PPS= 6 n（mW)。

图4.8 为当移相器的量化位数为1～8 位时，系统频谱效率与能量消耗的关系。从图4.8 中可以看出，在量化位数B 为1～4 位时，离散混合预编码系统的频谱效率逐渐增加，此时整个系统所消耗的能量也逐渐增加。当移相器的量化精度B 为4～8 位时，系统的频谱效率保持不变，然而系统能耗逐渐增加。当移相器的量化精度较小时，系统的频谱效率会有一定的增加，与图4.7 最后结果相同，当量化精度达到一定精度后，系统的频谱效率保持不变。对于系统的能量消耗，由于其与移相器的量化精度呈线性关系，当移相器的量化精度增加时，系统的能量消耗也逐渐增加。可以得出以下结论：适当的增加移相器的量化精度可以明显提高系统的频谱效率，但当移相器的量化精度过高时会引起不必要的能量消耗。

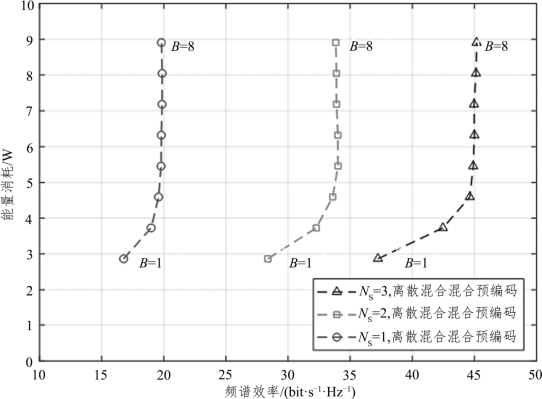
图4.8　系统频谱效率与能量消耗的关系