【摘要】：因为MG相对于RG转动了θ角，若RG与云纹的倾角为φ，则由图可见，φ与θ的关系为θ+2（φ-θ）=π，故图9.6.3由纯转动产生的云纹由此可见，当转角θ很小时，云纹相对于RG的倾角φ≈。在图9.6.2和图9.6.3中，MG变形或旋转之前，其栅线与RG栅线是相互重叠的，这时若对这些栅线按顺序编号，则显然两栅叠在一起的栅线序号是相同的。
仍设两片栅板的栅线是等间距的，并假设试件栅MG不产生线位移，仅相对于基准栅RG转动了一个角度θ（见图9.6.3）。这时基准栅与试件栅的栅线相交叉，在MG与RG二者栅线交叉点的连线上形成亮带条纹，此亮带云纹平分MG与RG二者栅线形成的菱形的钝角。当基准栅的栅线穿过试件栅的栅线之间的区域时，则遮挡了透过的光线，于是在亮带云纹之间形成暗带云纹。由图可知，亮带云纹间距δ近似为
。因为MG相对于RG转动了θ角，若RG与云纹的倾角为φ，则由图可见，φ与θ的关系为θ+2（φ-θ）=π，故
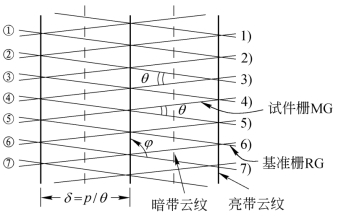
图9.6.3 由纯转动产生的云纹
由此可见，当转角θ很小时，云纹相对于RG的倾角φ≈
。这种云纹图案的特点可概括如下：(www.xing528.com)
①云纹几乎与栅线垂直，而与主方向几乎平行，整个云纹族只代表一个角位移；
②云纹是试件栅在垂直于参考栅栅线方向即主方向位移的等值线；
③云纹是相互平行和等间距的。
在图9.6.2和图9.6.3中，MG变形或旋转之前，其栅线与RG栅线是相互重叠的，这时若对这些栅线按顺序编号，则显然两栅叠在一起的栅线序号是相同的。MG变形或转动后，同一云纹恰好是RG栅线序号与MG栅线序号相减为常数的交点的连线，故称这些云纹为相减云纹（Subtractive Moiré）。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
