散斑干涉计量及其应用

散斑干涉是指被测物体表面散射光所产生的散斑与另一参考光相干涉，参考光可以是平面波或球面波，也可以是由另一种散射表面产生的散斑。当物体产生运动（位移或形变）时，干涉条纹将发生变化，由此可测量物体的运动或变化情况。前已指出，散斑计量学包括两大类别，即散斑照相术和散斑干涉术，两者都涉及干涉现象。前面介绍的用二次曝光散斑图进行的测试，就是利用的散斑照相术，但散斑照相术与散斑干涉术也是有区别的。概括说来，如果在两个图像上存在某些区域，其各自的散斑图样之间相关性良好，就把这种方法称为散斑照相术（Speckle Photography）；如果条纹的形成是由于两个图像之间散斑图样相关性的起伏造成的，而不论两图样的相关区域之间有否移动，这种方法就称之为散斑干涉术（Speckle Interferometry）。

下面以散斑剪切（错位）干涉术（Speckle Shearing Interferometry）为例进行讨论。这种技术可以直接显示出位移导数的等值线，故特别适用于应变分析。

1.散斑错位干涉的基本原理

实现散斑错位干涉的方法很多，下面以双孔径散斑错位干涉为例说明其原理。如图9.5.1所示，待测物体用准直激光束照明，在透镜前面放置双孔径板，两小孔相对于光轴对称布置，两孔径间距为t，小孔直径为d，要求t＞d。记录用底片放置在像面后Δv处，这样物面上一点经过透镜后变为两个像点，彼此相距Δxi=。由于孔径的直径d很小，致使焦深很长，故两个像点均处于适焦的状态。反之，对底片平面上给定点的散斑产生贡献的光线，来自物面上彼此分离的间距为Δx0的两个相邻物点，且

图9.5.1　双孔径散斑错位干涉仪

式中，M是透镜的横向放大率。底片上该点的光强度为

式中，a（x）表示x轴上位于x点附近小面元所散射的光在底片平面上产生的实振幅；φ是a（x）与a（x+Δx0）之间产生的位相差。物体发生微小形变后，底片上该点的光强为

式中，δ是由于物体变形引起x点和x+Δx0点相对位移所产生的纯位相变化。底片上记录的总光强度可表示成

当δ=2Nπ（N=0，1，2，…）时，I最大，当δ=（2N+1）π（N=0，1，2，…）时，I最小，从而产生干涉条纹。

2.空间滤波

由于物面上各点发生的运动状态不完全相同，上式所描述的是频率变化型的条纹图样。相对于来说，是快变化的。所以这种条纹图样要经过空间滤波处理后才能看到，其滤波系统如图9.5.2所示。激光束经扩束后由透镜L1聚焦到平面P上，该平面即是点源的像面。由傅里叶变换关系知，当散斑底片置于透镜和此像面之间时，在该像面上将获得散斑图样的傅里叶变换频谱，而散斑图样将成像于其频谱面的后方。通过在频谱面上插入滤波孔径，在其后的像面上显示出条纹图样。

图9.5.2　空间滤波系统光路图

式（9.5.4）中的δ可由下列的计算得到。对最初位于x处的物点因其位移L（x）所引起的散射光的位相变化为

式中，各为观察方向与照明方向的单位矢量（见图9.5.1），λ为激光波长。同样，对最初位于x+Δx0处的物点，由位移L（x+Δx0）引起的散射光的位相变化为

(www.xing528.com)

遂由x点和x+Δx0点相对位移产生的纯位相变化为

令L（x）的分量为u（x）、v（x）、w（x），的各分量由图9.5.1所示，有

则由式（9.5.7）得

由此可见，δ与位移导数相关联，从而条纹图样将反映位移导数的等值线。应用滤波小孔，让频谱面上的一个亮斑通过，则在成像透镜L2的像面上呈现一组散斑干涉条纹。令δ=Nπ，则由式（9.5.9）得

式中，N为条纹级次，由测点位置决定。当N为偶数时得明条纹，N为奇数时得暗条纹。

为了同时测出和，就要求有两个方程联立求解，为此要从两个不同的照明方向θ1、θ2记录两组条纹图样，这时得到

两式联立求解，最后得

式中，N1、N2分别为对应照明角θ1、θ2的条纹级次。对于不同的测试点，N1、N2的值将有所不同。

若选择θ2=-θ1（对称光路），则在同等加力条件下，有

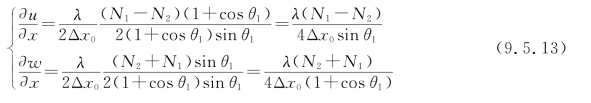
对于y方向的错位干涉，公式形式是一样的，并且可以取Δy0=Δx0=，同时采用4孔径板进行测试（见图9.5.3）。

图9.5.3　四孔径散斑错位干涉

3.计算机程序

根据上述各公式编写的计算机程序，见本章参考文献[8]第6章。该程序采用Fortran语言写成，主要用了两个语句函数和多维数组，比较简洁。