信息光学理论与应用：利用双散斑图系统测量空间位移

容易理解，图9.4.1的光路布置中，对与观察方向正交的面内位移较敏感，而对其离面位移则是不敏感的。因此，为了测试任意的空间位移，必须发展新的测试方法。新方法的要点是利用了矢量的投影变换，通过测量面内位移来计算空间位移，并把位移矢量的投影变换关系用矩阵方程表示，便于计算机编程，从而实现快速计算。

1.矢量的投影变换矩阵

在图9.4.5中，令LP代表位移L在以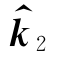为法线的平面上的投影，则有

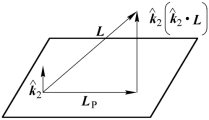
图9.4.5　矢量的投影

若把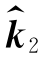视为观察方向，则LP便是垂直于观察方向的面内位移，当以待测点作为坐标原点时，则有

或写成

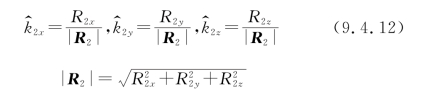
式中，R2为坐标原点（待测点）到观察点的空间矢量。将式（9.4.10）改写成矩阵式得

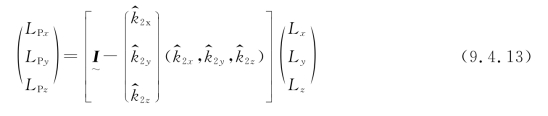
式中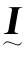，为3×3单位矩阵，式（9.4.13）可改写为

式中

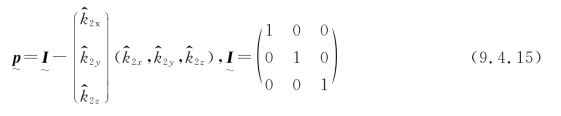
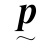称为矢量的投影变换矩阵，它将矢量L投影到法线为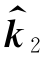的表面上以形成投影LP。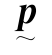只与R2有关，且具有下列特性（读者可自行证明）：

（1）对称，且；

（2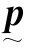）的行列式等于0，故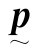是降秩矩阵，无逆矩阵。(www.xing528.com)

2.计算空间位移的公式

显然，仅仅依据位移矢量在某个平面上的投影不能确定空间位移矢量本身，至少要根据位移矢量在两个平面上的投影才能确定。解决的办法是：从两个不同的观察方向同时拍摄两张二次曝光散斑图，设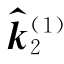、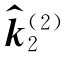代表两个观察方向的单位矢量，对每一个观察方向，可测得物点位移的一个投影（垂直于该观察方向的面内位移），即有

式中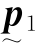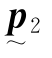，、为与两个观察方向相应的投影变换矩阵。把式（9.4.16）写成矩阵方程：

用转置矩阵左乘上式两端，并注意投影变换矩阵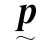的对称特点，则有

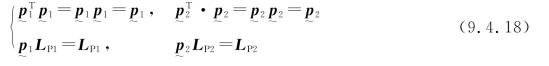
便得

式（9.4.19）即计算空间位移的公式，需要测量的是垂直于两个观察方向的面内位移和相应的空间矢量R2的各分量。无论位移是均匀的还是非均匀的，只要按照上述方法测量垂直于观察方向的面内位移，就可由式（9.4.19）算出空间位移。根据最小二乘法原理还可以证明，应用公式（9.4.19）求得的结果具有最小均方误差。

3.实验与计算实例

实验光路如图9.4.6所示，为了减少测量误差，采用了对称结构形式，将两路记录成像散斑的光路布置在入射激光光束两侧。将待测试物体置于可做微小移动的机构上，或放在沿水平方向和竖直方向都可同时加力的光弹仪上。二次曝光散斑图底片经显影、定影和漂白处理后，在图9.4.3后焦面翻拍成干涉条纹图样照片（图9.4.7），用以测出条纹间距Δt和条纹相对于y轴的取向角θ，再分别测定及。物距和像距的值由以下两式确定：

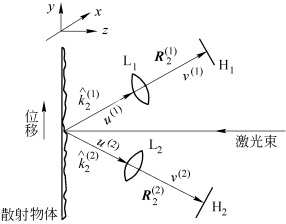
图9.4.6　用双散斑图测空间位移的实验光路

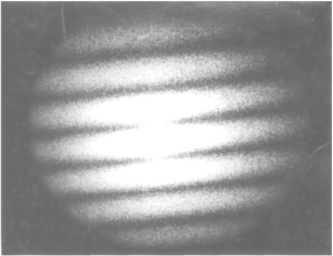
图9.4.7　散斑条纹图样照片

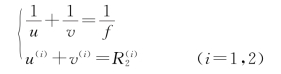
应用上述方法，测试了颅面骨的微小变位场，为口腔正畸提供了有用的数据；实验研究了四川某地区地质构造相似模型裂缝分布规律，从建立产气层顶面的三维位移场出发，据此预测了张性裂缝发育的有利区域，为有效地勘探和开发油气田提供了一定的实验依据。具体的测试方法见文献[8]第6章。