散斑图的处理方法-《信息光学理论与应用》

散斑图片的处理，通常采用两种方法，即逐点分析法和全场分析法。

图9.4.2表示逐点分析法（Point by Point Analytical Method）光路。用细激光束照明散斑图底片，在观察屏上将看到由被照明小区域“散斑对”产生的杨氏干涉条纹。相邻亮条纹（或暗条纹）的间隔Δt均满足下列关系：

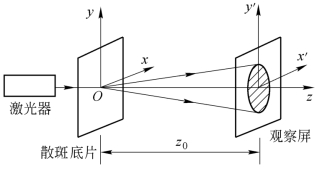
图9.4.2　逐点分析法的光路

式中，l为“双孔”间距（即位移量），且条纹取向与“双孔”连线（即位移方向）垂直；z0代表散斑底片与观察屏之间的距离。注意到上述位移是经过透镜（在记录时）放大了的值，故实际位移量应为

式中，u、v各为物距和像距。当位移的大小和取向不同时，条纹的疏密和取向也不同。

图9.4.3表示全场分析法（Full-field Analytical Method）的光路之一。将散斑图底片放在光信息处理系统中进行分析。为了分析方便，设“散斑对”相对于光轴对称排列，且其连线与x轴成θ角，则此散斑对可用一对δ函数表示成

图9.4.3　全场分析法的光路之一

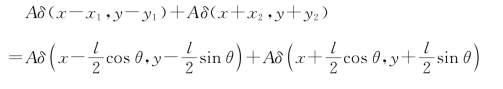
在变换平面上将得到它们的频谱。应用欧拉公式并令，经整理最后得

所以，变换平面上的光强分布可表示成

(www.xing528.com)

式中，I1=A2，而

式中，l是位移矢量，r是变换平面上的位置矢量。显然有

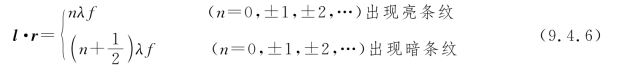
这些条纹分布在散斑图上，构成位移矢量l在r方向投影的等值线族。若位移场是均匀的（刚性位移），则由式（9.4.6）有

由此得垂直于位移矢量的一族直线条纹，条纹间距等于，与式（9.4.1）类似。

若位移场是非均匀的，一般在变换平面上看不到干涉条纹。这时需要在变换平面上安置一个滤波小孔。如图9.4.4所示，设滤波小孔位于水平位置（xf0，0），则在像面上凡是位移分量为

图9.4.4　全场分析法的光路之二

的点均出现亮条纹，由此得到水平位移相等的点的轨迹。当滤波小孔位于竖直位置（0，yf0）时，则像面上凡是位移分量为

的点均出现亮条纹，由此得到竖直位移相等的点的轨迹。滤波小孔位于任意位置时，可类似分析。