散斑光强分布函数：信息光学理论与应用

前面已指出，散斑场的光强分布具有随机性，故推导光强分布函数要应用统计光学方法。首先考虑自由空间传播散斑场，即研究激光被某个表面散射时形成的散斑，如图9.3.2所示，其中S为散射面，T为观察平面。假设散射面上共有N个独立的散射面元（N是一个很大的数），这些面元具有相同的宏观结构，仅仅在微观上有区别；并设入射光波是线偏振的单色光，且其偏振状态不因散射而改变。令

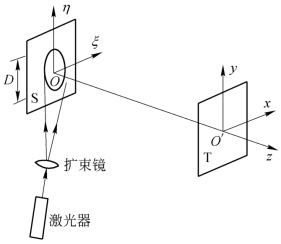
图9.3.2　自由空间散斑

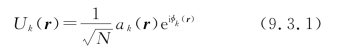
表示由第k个散射面元散射到观察点的基元光波复振幅（相幅矢量），其中表示此相幅矢量的随机长度，φk（r）为其随机位相，则由N个面元散射到观察点的各基元光波叠加以后，最后的复振幅为

显然，入射到散射面的相干激光，散射后物面光场不再是激光器发出的空间相干场，而是变成了严格空间非相干的，故式（9.3.2）中的各随机相幅矢量求和完全是随机的，如图9.3.3所示。可将复振幅的实部和虚部分别写成

图9.3.3　随机相幅矢量求和

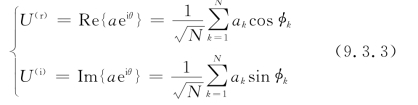
为了分析方便起见，设基元复振幅具有下列统计特性：

①每一个基元光波的振幅和位相是相互统计无关的，并且与所有其他基元光波的振幅和位相也是相位统计无关的，这是由于散射表面的随机涨落高度与随机反射系数之间不存在物理上的联系；

②对于一切k，随机振幅ak有完全相同的分布，其均值为〈a〉，二阶矩为〈a2〉；

③各位相φk在-π与+π之间的所有值上都是均匀分布的。

这样，当N足够大时，在观察点求得的光场U（r0）的实部和虚部是独立的，其平均值等于零，都是无规变量的高斯分布。事实上，由于ak和φk是相互独立的，且对一切k都有相同的分布，故其振幅U（r）的实部U（r）和虚部U（i）对系统的平均值可由下列两式计算：

又由于随机位相φk在-π与+π之间的所有值上都是均匀分布的，结果当N足够大时有〈cosφk〉=0，〈sinφk〉=0，从而

还可以证明，复振幅的实部和虚部是不相关的，因为有

而

所以有

由此可见，U（r）和U（i）二者是彼此独立的，且都是许多独立的随机贡献之和，故在N足够大的情况下，它们都是高斯型随机变量（Gaussian Random Variable），遂由高斯误差分布定律知，其联合概率密度函数（The Joint Probability-Density Function）为

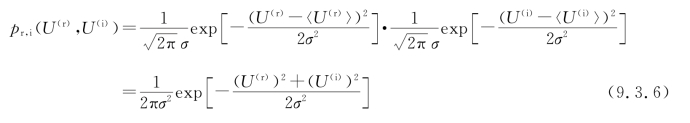
式中，σ称为复振幅的标准偏差，它是随机变量U（r）取值的弥散程度的量度，其平方值σ2称为方差。为了计算U（r）的方差，首先计算其实部和虚部的方差σ2r、σ2i。对于离散型随机变量x，方差定义为

而对于U（r）和U（i），因其〈U（r）〉=〈U（i）〉=0，故为了计算σ2r和σ2i，可等效地化为计算〈（U（r））2〉、〈（U（i））2〉。应用各个ak和各个φk的独立性，可以写出

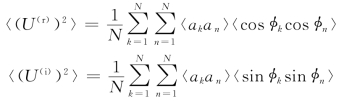
而由于各个φk在-π与+π之间的均匀分布，又有

因此可得到

于是，σ2又可写成以下表达式：

对于连续变化型随机变量U，方差可定义为

式中，pU（U）表示其分布的概率密度函数。经展开上式后算得

两个随机变量U、V的相关定义为(www.xing528.com)

式中，pUV（U，V）为其联合分布的概率密度函数。

此外，定义两个随机变量U、V的协方差（Covariance）为

上式右端经展开后算得

或写成

如果两个随机变量U、V是相互独立的，则〈UV〉=0，从而CUV=0；反之，当CUV≠0时，U、V便不相互独立，而是存在着一定的关系。定义：

为随机变量U、V的相关系数。式中σU、σV分别表示U、V的标准偏差。

归纳起来可以看到，合成散斑场的复振幅U（r）是一个随机变量，其实部和虚部彼此独立，并具有公式（9.3.4）、（9.3.5）和（9.3.8）所述的特性（即均值为零、互不相关和方差相等）。我们把满足上述条件的随机变量称为圆型复数高斯随机变量（Circular Complex Gaussian Random Variable），其等值概率密度线是复平面上的一些圆，如图9.3.4所示。

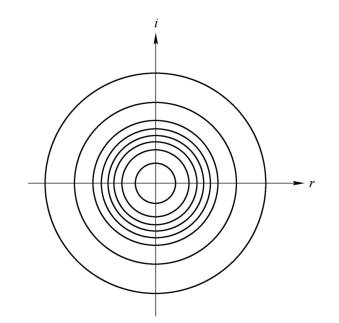
图9.3.4　（r，i）平面上的等概率密度线

下面再来讨论合成散斑场的光强度I和位相θ的统计分布。它们与复振幅的实部和虚部用下列关系式联系：

或者等价地：

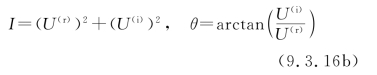
为了求得I和θ的联合概率密度函数，可利用多元随机变量的变换方法。即令

式中

‖J‖称为变换的雅各比行列式（Jacobian）。将式（9.3.16a）代入式（9.3.18）算得‖J‖=，现将此结果和式（9.3.6）代入式（9.3.17），便求得强度和位相的联合概率密度函数为

而强度的边缘概率密度函数（Marginal Probability-Density Function）为

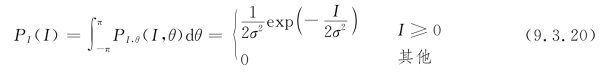
同样，位相的边缘概率密度函数为

由此得出偏振散斑场中的光强分布遵守负指数统计（Negative Exponential Statistics），而位相则遵守均匀统计（Uniform Statistics），并且

即在散斑场中任一点处光强度和位相是统计独立的。根据公式（9.3.20），并利用积分公式：

令其中n=1，a=1，还可以求出光强的平均值：

因此公式（9.3.20）还可以化为

图9.3.5为PI（I）的曲线。显然，散斑图中光强为零的概率密度最大，而多数可能的光强近似为零，即出现暗斑的地方较多。

图9.3.5　散斑图光强的概率密度函数