第4版：测定物体微小振动的信息光学应用

分析和测量微幅振动，也是全息干涉计量的一个重要应用领域。用全息照相方法可以测量振动物体表面各点的振幅矢量、共振频率、振动位相以及进行振动的模态识别。这些测量对于分析疲劳、断裂事故，改进机械结构设计、机床的加工精度以及声换能器的质量等，都具有十分重要的实用意义。

在9.1节中已讨论到，对于做简谐振动的物体，其时间平均全息图重现像的光强度按零阶贝塞尔函数的平方分布，即

式中

其中，A表示振幅矢量，K为灵敏度矢量。

如果振动物体是一块平面薄板，其上各点的振动方向与板面垂直，则只有振幅的量值是未知的，这时根据式（9.2.45）、式（9.2.46）便可简单地由J0（φ）、J1（φ）的根及测点的空间位置，求得由时间平均干涉图中明暗条纹分布相对应各点的A值。如果振动物体的表面为曲面，则其上各点的振动方向各不相同，这时为了讨论方便，应假定物体上各点的振幅为一个三维空间矢量A。为了测定A，需要建立起类似于式（9.2.46）的3个标量方程：

再联立求解。式（9.2.47）如采用分量表示，则可表示成

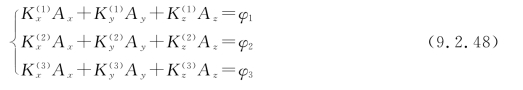
其中

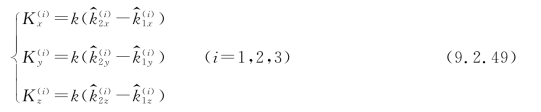
K（i）（i=1，2，3）代表3个不同方向的灵敏度矢量；k=。(www.xing528.com)

将式（9.2.48）写成矩阵形式，即

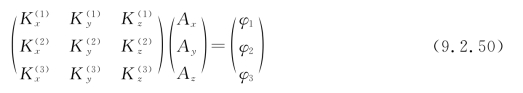
或简写成

容易求得

式（9.2.52）即为求解振幅矢量A的公式。

具体测试时可采用单张全息片记录三重像的办法来建立式（9.2.47）中的3个方程，并通过编程计算微小振幅。

式（9.2.15）、（9.2.26）、（9.2.41）和（9.2.52）具有若干共同特点，可简要概括如下。

（1）它们将待测物体的微小运动量与观察点、照明点源的较大坐标值及条纹漂移信息联系起来，通过测量较大的量来确定微小的量，这样就有利于提高测量精度。

（2）它们都应用了矩阵形式，便于构成计算机程序，并且各公式的形式都极相似，这样就减少了编程上的许多麻烦。

（3）还可以证明，这些公式都符合最小二乘法原理，因而用它们测试算得的结果都具有最小均方误差。