测定均匀应变的方法-信息光学理论与应用

在实验力学中，精确测定物体的应变具有很重要的意义，因为它影响到机械结构或零件的强度、安全和寿命，因而也联系到结构设计误差。在构造力学模拟实验研究中，通过测定地质结构相似模型的应变场，可判定地质构造中存在的裂缝位置，从而为油气勘探提供依据。应变是与位移的导数有关的动态量。故研究均匀应变，可从对条纹定位函数求导（取梯度）着手。令此梯度函数为条纹矢量（Fringe Vector），即

由于在直角坐标系中有

所以对式（9.2.28）微分运算的结果，得到一个含有18项的方程式，经整理可以表示成下列矩阵形式：

或

式（9.2.29b）可简写成

式中

而

式（9.2.30）是条纹矢量理论中的一个基本关系式。

从弹性力学中知道，应变是一个张量，完全描述它需要9个分量，故应变张量（Strain Tensor）可以按以下关系定义：

其中

表示法向应变（Normal Strain），而

表示切应变（Shearing Strain）。显然有

因此应变张量是对称张量，它的9个元素中只有6个元素是独立的。

如果物体除发生切应变外还发生旋转，则物体上任一点Q因旋转所引起的位移表示为(www.xing528.com)

其中，θ表示微小转角，R表示由坐标系原点到Q点的空间位置矢量。式（9.2.36a）可写成下列分量方程：

对上列各式求导，并考虑到x，y，z及θx，θy，θz是两组各自独立的变量，经整理后便得到物体在发生应变过程中，绕x、y、z轴转动的各分量为

因此在做微小运动的情况下，物体的转动也能用位移的导数来表示。将式（9.2.37a）写成矢量形式有

θ称为旋转矢量（Rotation Vector）。遂由式（9.2.31）、式（9.2.33）、式（9.2.34）和式（9.2.37）易知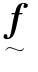，可表示成

式中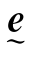，称为应变矩阵（或应变张量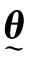）；称为旋转矩阵，它是由θ的各分量构成的一个反对称矩阵；而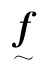称为变换矩阵。由于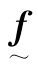可形式地表示成

故由式（9.2.33）、式（9.2.34）、式（9.2.37a）、式（9.2.38）和式（9.2.39）可得下列关系：

因此，只要能求出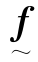，则物体发生的应变和旋转便可求得。

数学推导表明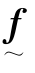，可以用下式表示：

式中

角标1，2，…，r代表在多次观察中的各次观测值，而

其中，Ri是由照明点源到待测点P之间的距离，R0是待测点到观察点的距离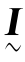，是3×3单位矩阵，⊗表示两个矢量之间的矩阵乘积，其定义如下式：

乘积的结果得到一个矩阵，其元素是两矢量各分量的所有可能的9种乘积。