测定刚体微小转角与平动|信息光学理论与应用

刚体的普遍位移可以分解为转动与平动两部分。因此，刚体上任一点P的总位移可表示为

式中，L0代表平动位移；θ表示刚体的微小转角；R是由坐标系原点到P点的空间位置矢量。令

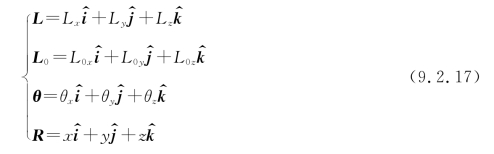
则式（9.2.16）可用分量形式表示为

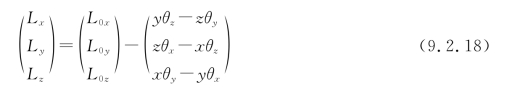
或改写成

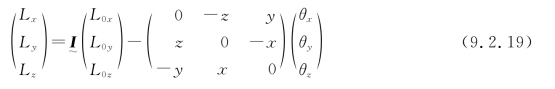
或写成更紧凑的形式：

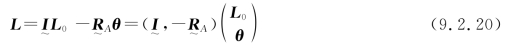
式中

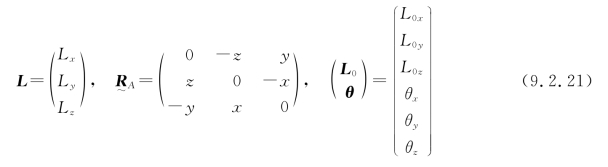
代表由R的分量构成的反对称矩阵，其行列式等于零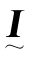代表3×3单位矩阵。

式（9.2.20）中的L可按9.2.1节介绍的方法测量和计算。遂由式（9.2.20）出发对测试点算出L后，便可求解L0、θ。但L0、θ都是矢量，要解出它们，至少需要两个矢量方程。这些方程可通过选择两个测试点建立起来，相应地有

L1=L0-R1×θ,L2=L0-R2×θ

或写成矩阵形式：(www.xing528.com)

式中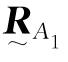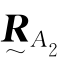，、的意义与式（9.2.21）中的类似，各自代表由两个测试点的空间位置矢量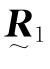、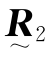的分量构成的反对称矩阵，考虑到它们的行列式都等于零，并且有

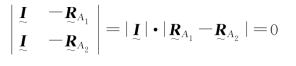
故式（9.2.22）右端的方阵是降秩的，它没有逆矩阵。因此，为了确定刚体的转动与平动，至少需要3个测试点。又为了减少由全息干板的有限尺寸以及选择测试点位置的任意性所带来的测量误差，最好选择n＞3个测试点。对每个测试点可得到类似于式（9.2.20）的一个方程，n个测试点就有n个方程，这样就形成了一个超定方程组，写成矩阵方程即为

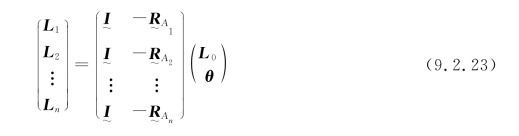
令

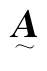是3n×6矩阵，这时式（9.2.23）可改写成

用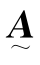的转置左乘式（9.2.25）两端，最后求得

式（9.2.26）就是测定刚体微小转动与平动的公式。求出L0x、L0y、L0z及θx、θy、θz后，应用以下公式：

便可算出刚体的平动与微小转角的量值。