用二次曝光法测定三维位移场-信息光学理论与应用改进版

测定位移的基本公式为

式中Ω代表待测点移动前后由照明点源发出到达观察点的两束物光的位相差，L表示位移，K是灵敏度矢量（Sensitivity Vector），其定义为

式中k=（λ为激光波长）各代表沿观察方向和照明方向的单位矢量。在以待测点P作为坐标原点的情况下（图9.2.1），有

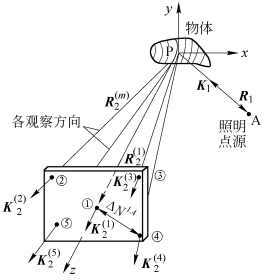
图9.2.1　五点观察法

式（9.2.1）可按图9.2.2导出。设物点P发生位移后移动到P′点，位移矢量为L，则由点源A经P点与P′点到达观察面给定点的位相差可与灵敏度矢量和位移矢量的标积联系起来，如图9.2.2所示。其中K1、K2分别是P点移动前由照明点源指向待测点的传播矢量和由待测点指向观察者的传播矢量；K1称为照明矢量，K2称为观察矢量。K3、K4分别是P点移动后的相应量。

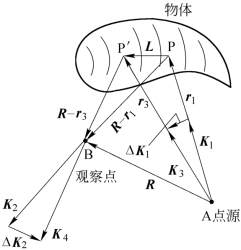
图9.2.2　位移矢量与相位差的关系

P点移动前后到达观察者的两束物光的位相分别是（设点源A处的初位相等于零）：

遂由观察者测得的位相差是

由图9.2.2可知

故由上列各式综合整理得

在实际系统中，|r1|、|r3|≫|r3-r1|=L（微小位移），可以认为ΔK1⊥r3、ΔK2⊥（R-r3），于是，式（9.2.7）中的最后两项标积为零，从而有

(www.xing528.com)

上式就是测定微小三维位移的公式，也是全息干涉条纹定量解释的基础。当Ω=2Nπ（N为整数）时，将得到明条纹；当Ω=（2N+1）π时，得到暗条纹；当Ω为某一常数时，即确定了物体表面上某个条纹灰度的位置。Ω称为条纹定位函数（Fringe-locus Function），N称为条纹级次（Fringe Order）。

在导出测定位移的基本公式（9.2.8）时，实际上采用了下面的模型：物体表面由大量的点散射体构成，当表面上任一点P位移到点P′时，由点P发出的光和由点P′发出的光产生干涉形成全息干涉条纹；点P发出的光和物面上其他点发出的光不会发生干涉。这个模型是方便和充分的。

式（9.2.8）把观察-照明条件及条纹级次与未知位移联系起来。具体计算时，由于L是矢量，至少需要3个独立方程式联解才能求得；同时，由于条纹的绝对级次通常不易知道，还须引入相应于某任一观察方向的条纹级次的一个相加常数Ω0。换言之，为了确定L（Lx，Ly，Lz）及Ω0，至少需要4个独立方程式。这些方程式可以通过4次独立观察建立，每次以不同的方向观察便得到一个类似于式（9.2.8）的方程。由于全息干板尺寸有限，再加上对观察点位置的选择有任意性，因此，如果只选择4个观察点建立方程组来测量、计算，将产生较大的误差。为了减少实验误差，普遍都经过大于4次的观察，这样就形成了测定L和Ω0的一个超定方程组（Overdetermined set of Equations）：

式中

r是观察总次数（r＞4）。ΔN1，m代表观察者由沿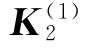方向连续地改变到沿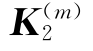方向观察时，所观察到的通过待测物点的条纹漂移数（见图9.2.1），显然有ΔN1，1=0。当研究物面上不同的测点时，如果物面不太大，应用准直光照明物面是方便的，这时矢量K1是常数，式（9.2.10）中就采取了这种方式。

方程组（9.2.9）可做适当移项，并改写成矩阵形式：

或简写式

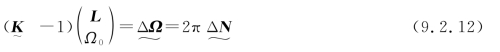
其中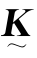，（-1）是r×4矩阵，是4×1（列）矩阵，是r×1（列）矩阵。令

则式（9.2.12）可重写成

上式表明，欲计算L、Ω0，须求出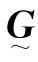的逆矩阵，而为了求得逆矩阵，原矩阵应是方阵且满秩，为此，可用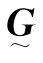的转置矩阵左乘式（9.2.14）两端，最后得

式中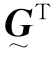，表示矩阵的转置（下同）。式（9.2.15）就是测定位移的最后公式，是通过建立超定方程组并转换成矩阵形式导出的，这样就便于编写计算机程序做快速计算。同时，式（9.2.15）将待测物点的微小位移量与照明点源、观察点的较大的坐标值以及条纹漂移数联系起来，这样就可以通过测量较大的量来确定微小的量，有利于提高测量精度。

具体测试三维位移场（以及本节后面讨论的其他测试项目）的实验步骤、数据处理和编程计算，见文献[8]第5章。