时间平均全息干涉术在信息光学中的应用

时间平均全息干涉术（Time-Averaged Holography）是指对周期振动的物体做较长时间单次曝光的全息照相，曝光时间一般远大于物体的振动周期。因此，全息底片上记录了物体振动过程中不同状态的许多全息图，并且与各种状态在曝光期间出现时间的长短成比例分配。虽然在记录过程中各个全息图是依次记录的，但它们却被同时重现，因而能彼此干涉。这样的全息图实际上是记录了由物体散射到全息底片表面的光波的时间平均的复振幅，因此称为时间平均全息图。当物体做正弦振动时，在靠近它的两个最大位移位置，即速度为零处，要占用较多的时间，由于物体的振动频率通常达数百至数千赫兹，而全息记录时间在数十秒范围，故这两个运动状态在整个曝光期间内积累的结果将占据优势，所以主要是记录了物体的这两个运动状态。于是，可以定性地说，以这种方式得到的时间平均全息干涉图样与一张用二次曝光法得到的全息干涉图样有相似之处，它显示了上述两个极端位置之间（处于位相相反状态）物体位移的轮廓线（节点或节线）。

当从数学上处理时间平均法中所发生的物理现象时，为简洁起见，假定只讨论物体做正弦振动的情况，这时物光场可以用下式表示为

式中，ω为振动角频率，z2为任一物点的振幅，z2cosωt代表t时刻物点的振动位移，γ是照明角与观察角的函数。例如，在图9.1.2所示的悬臂梁振动的情况下，γ=cosθ1+cosθ2。

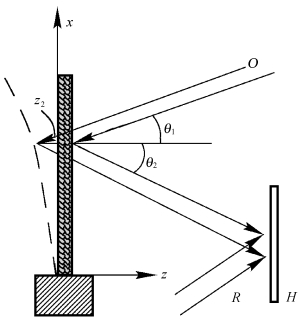
图9.1.2　悬臂梁的振动

由于时间平均全息图记录了在曝光期间出现的所有的物光场，而这些物光场按每一振动周期重复出现，因而求时间平均时只需求一个周期的平均，即

式中，时间平均积分称为正弦振动的特征函数，记作MT。于是，重现像复振幅与AOMT成正比。相应地，其光强度可表示成

根据贝塞尔函数的积分表达式：

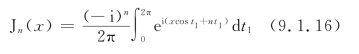
当n=0时，有

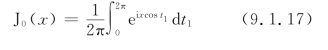
对周期为T的函数进行变量代换，即令t1=ωt，则dt1=ωdt，故式（9.1.17）变成

将式（9.1.18）与式（9.1.14）相比较，得(www.xing528.com)

故式（9.1.15）又可写成

即时间平均全息干涉图重现像的光强度按零阶贝塞尔函数的平方分布，其分布曲线如图9.1.3所示。由图上看到，当零阶贝塞尔函数的自变量等于零时（即z2=0），函数取最大值。因此在重现像的振动图样中，不运动的区域（节点或节线）将显示出最明亮的条纹（称为零阶明条纹），它比其余的明条纹要亮得多。其余明条纹的位置由一阶贝塞尔函数的根给出，因为根据求极值条件及贝塞尔函数的性质，有

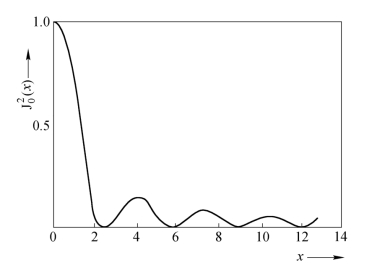
图9.1.3　J20（x）曲线

暗条纹的位置即由零阶贝塞尔函数的根给出。表9.1.1给出了J0（x）和J1（x）的前10个根。

表9.1.1　J0（x）和J1（x）的前10个根

由图9.1.3中曲线还可看到，随着明条纹级次的增加，其强度是递减的。这说明它与二次曝光法所得的干涉条纹不同。同时，由于J20（x）调制条纹，使其对比度逐级下降。

根据时间平均全息图上干涉条纹的分布，可以分析振动物体各部位的振幅分布。这种方法已发展成为全息振动分析的一种成熟技术，并在汽车工业、飞机制造业和机床制造业中获得良好的应用，这对于改进机械结构的设计、分析疲劳和断裂事故以及改进机床的加工精度等都有十分重要的应用价值。

如图9.1.4所示是拍摄的激振小提琴的时间平均全息干涉图，据此对小提琴发生的振型和各部位的振幅分布进行了分析和测试，从而指导普及型小提琴的制作。

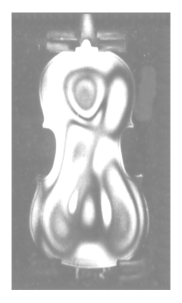
图9.1.4　激振小提琴的时间平均全息干涉图