信息光学理论与应用中的光学微分处理方法及效果

在6.1节中已指出，利用高通滤波器可以使图像边缘增强，但由于使用高通滤波器时光能量损失很大，因而像的能见度大大降低，减弱了信号。但利用光学微分方法可以得到较满意的结果。

1.光学微分光路系统及其基本原理

光学微分光路系统仍采用4f系统，将待微分的图像置于输入面的原点位置，将微分滤波器置于频谱面上，当位置调整适当时可在输出面上得到微分图形。

设输入图像为t（x，y），其傅里叶变换谱为T（fx，fy），由式（1.6.19）知

显然，如置于频谱面上的滤波器的滤波函数为

则可实现对图像的光学微分。实际上，微分滤波器的振幅透过率只需要满足正比于x2，即可达到光学微分的目的（见习题7.4）。

2.微分滤波器的制作方法

微分滤波器可用多种方法制作，例如，用光学全息方法或计算全息方法制作。这里仅介绍前一种方法。这种全息微分滤波器实际上是一个复合光栅，它由两套空间取向完全相同、空间频率差为Δf0的一维余弦振幅光栅叠合而成，拍摄光路仍如图5.8.3所示，采用两次曝光法，并将干板架置于一个能在水平面内转动的平台上，两次曝光之间使平台旋转一微小角度Δθ，设第一次曝光得到光栅的频率为f0，第二次曝光得到光栅的频率为f′0，胶片经显影、定影等处理后，便做成了光学微分滤波器。显然，此复合光栅包含了两种频率，为书写简洁起见，设其初始位置时的透过率函数为

把它放到4f系统的频谱面上，这样，置于输入面原点的物的频谱受到两个一维余弦光栅的调制，当其受第一次记录的光栅调制后，在输出面上可得到3个衍射像，其中零级像在原点，正、负一级像对称分布于两侧，距原点的距离l=±λff0，f为透镜焦距。受第二次记录的光栅调制后，在输出面上得到另一组衍射像，其中除零级像与前一个零级像重合外，正、负一级衍射像也对称分布于两侧，与原点的距离l′=±λff′0。由于Δf0=f′0-f0很小，故l与l′的差Δl=λfΔf0也很小。从而使两个对应的±1级衍射像几乎重叠，使沿x方向只错开很小的距离Δl（见图7.6.1）。当复合光栅沿x2轴移动周期（即）时，将引起光栅条纹的初位相变化，而当其移动Δx2时，则其初位相变化由下式确定：

由此引起两个同级衍射像的相移量为

(www.xing528.com)

从而导致两者之间有一附加位相差：

与通常的位相差关系式Δφ=Δx相比较，式（7.6.10）引入了一个“等效波长”（Equivalent Wavelength）的概念。令Δφ=π，得

这时两个同级衍射像正好相差π位相，这样相干叠加时两者的重叠部分（如图7.6.1中阴影部分）相消，只剩下错开的图像边缘部分，从而实现了边缘增强。转换成强度时形成亮线，构成了光学微分图形，如图7.6.2所示。若将复合光栅条纹在面内旋转90°，便可得到对y方向的微分。

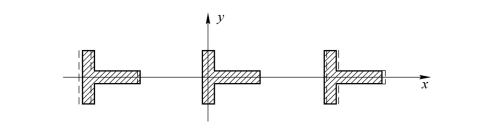
图7.6.1　在输出平面上得到的图像微分运算结果示意图

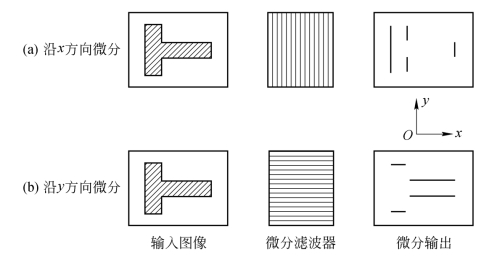
图7.6.2　光学微分处理过程示意图

上述方法只能进行一维微分运算，即得到或。要想进行二维微分，还必须利用更复杂的微分滤波器。

光学微分的原理并不复杂，这里仍以一维情况为例做一简要说明。由式（7.6.7）可知，只要在4f系统的频谱面上放置一滤波器，使其滤波函数H（fx，fy）正比于，亦即正比于x2，当输入图像的频谱T（fx，fy）投射其上时，就可得到式（7.6.7）右边的乘积，再经过透镜L2进行一次傅里叶逆变换，便可在输出平面上得到原函数的微商。本系统所利用的复合光栅，其透过率函数在Δf0很小时可认为正比于x2，因此用它执行微分滤波器的功能是合适的。

3.光学微分的应用

人的视觉对于物的轮廓十分敏感，轮廓也是物体的重要特征之一。只要能看到轮廓线，便可大体分辨出是何种物体。因此，如果将模糊图片（如透过云层的卫星照片、雾中摄影片等）进行光学微分，勾画出物体的轮廓来，便能加以识别。这在军事侦察上十分有应用价值。

微分滤波器还可用于对位相物体进行光学微分，以勾画出位相物体的边缘。据此可检测透明光学元件的内部缺陷或折射率不均匀的问题，也可用于检测位相型光学元件的加工是否符合设计要求。