在成像过程中,一张照片可能由于种种原因变模糊,如成像系统的像差、目标和底片的相对运动、大气扰动等。但不论属于哪种原因,像模糊都可以归结为系统传递函数的缺陷。如果在相干光学滤波系统(如图6.1.6的4f系统)中,在其频谱面上对系统传递函数做适当的补偿,则有可能在输出平面上获得清晰的像。这一相干光学处理过程称为图像消模糊(Image Deblurring)。
1.基本原理
设物的光场分布为f(x,y),造成模糊像的系统的点扩展函数为h(x,y),由于像函数g(x,y)是物函数与点扩展函数的卷积:
![]()
该卷积的结果就使得图像的细节变得模糊。因此,图像消模糊的问题就变成了去卷积(Deconvolution)的过程。前已指出,在空域中实现卷积运算较为困难,但做频域处理却非常简便。其办法是将模糊图像置于4f系统的输入平面上,这时在频谱面上的复振幅分布为
G(fx,fy)=F(fx,fy)H(fx,fy)
式中,G(fx,fy)、F(fx,fy)和H(fx,fy)各为函数g(x,y)、f(x,y)和h(x,y)的频谱。若选择滤波函数满足下列条件:
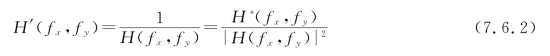
则滤波后的频谱变为
![]()
这时传递函数等于1,像频谱与物频谱完全一样,亦即恢复了原来物函数的频谱。再经一次傅里叶逆变换,在4f系统的输出面上便得到f(x,y)的清晰像。滤波函数满足式(7.6.2)的滤波器便称为逆滤波器(Inverse Filter)。(https://www.xing528.com)
2.逆滤波器的制作方法
由式(7.6.2)看出,逆滤波器由两部分组成,即H*(fx,fy)和![]() 。因此,仿照7.2节,可以用制作傅里叶变换全息图的方法,先利用点扩展函数h(x,y)制作一个全息滤波器,使其滤波函数为H*(fx,fy),然后用普通照相方法在h(x,y)的频谱面上用干板进行拍摄,记录它的频谱像,制作一个振幅滤波器,使其滤波函数为
。因此,仿照7.2节,可以用制作傅里叶变换全息图的方法,先利用点扩展函数h(x,y)制作一个全息滤波器,使其滤波函数为H*(fx,fy),然后用普通照相方法在h(x,y)的频谱面上用干板进行拍摄,记录它的频谱像,制作一个振幅滤波器,使其滤波函数为![]() 。只要记录h(x,y)的功率谱,并小心处理使照相胶片的γ=2,则其振幅透过率就与
。只要记录h(x,y)的功率谱,并小心处理使照相胶片的γ=2,则其振幅透过率就与![]() 成比例。使用时将两者对正紧密叠合在一起,便得到了逆滤波器。
成比例。使用时将两者对正紧密叠合在一起,便得到了逆滤波器。
应当注意:制作逆滤波器需要预先知道产生像模糊的点扩展函数h(x,y),而这一点往往难以做到,再加之胶片动态范围的限制,使得只能得到近似的逆滤波函数。此外,逆滤波过程与成像过程一样,也受到系统空间带宽积的限制,因此,期望用逆滤波器的办法实现图像超越衍射极限的复原是不现实的。
【例1】摄影时由于不小心,横向抖动了2a,形成两个像的重影,试设计一个改良此照片的逆滤波器。
【解】在此情况下引起成像缺陷的点扩展函数为
![]()
其傅里叶变换传递函数为
![]()
遂得逆滤波器的滤波函数为
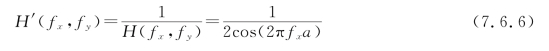
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




