图像识别卓越成果|信息光学理论与应用

特征识别的方法是将待检测的物函数f（x1，y1）放在相干光学处理系统（典型的如4f系统，见图6.1.6）的输入平面P1上，而将含有特征信号h（x1，y1）共轭谱H*（fx，fy）的全息匹配滤波器置于频谱面P2上〔H*（fx，fy）实际为原地制作的〕。这时挡去参考光，只让物光通过匹配滤波器。设物函数的频谱函数为F（fx，fy），则在P2后表面的复振幅分布为F（fx，fy）τ，其中τ为全息匹配滤波器的复振幅透过率，在线性记录条件下，该全息匹配滤波器的复振幅透过率与曝光强度I成正比。由此得P2后表面的复振幅分布为

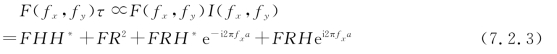
而（在反演坐标下）在P3平面上的复振幅分布g（x3，y3）为

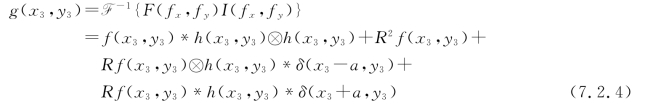
式中重要的是第3、4项，它们分别是输入的物函数与特征信号的互相关和卷积，其中心在（±a，0）处，如图7.2.2所示。在特征识别中，我们关心的是相关。

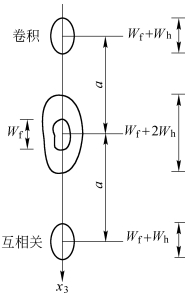
图7.2.2　在P3平面上各输出项的位置

若待检测的物函数图像中包含特征信号和相加性噪声，则

其频谱函数为

经H*（fx，fy）滤波后的频谱为

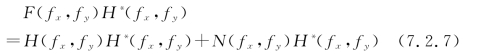(www.xing528.com)

再经透镜L2作傅里叶逆变换后，在输出平面P3上的复振幅分布为

式中最后一项能量比较弥散，只有特征信号的自相关在相应位置处存在鲜明亮点。至于式（7.2.4）中的第4项，由于卷积的结果获得一个模糊的图像，远不如相关亮点鲜明。因此，利用匹配滤波相关检测方法就可以从带有噪声的信息中提取出有用信息，达到特征识别的目的。

为了使相关项（包括卷积项）与中心项不相互重叠，以避免对识别的干扰，应适当选择参考光倾角的大小。设待检测物函数f（x1，y1）和特征信号h（x1，y1）沿x3轴方向的宽度分别为Wf和Wh，而由式（7.2.4）知，其中前2项的宽度分别为Wf+2Wh和Wf，相关项和卷积项的宽度均为Wf+Wh，由图7.2.2可见，欲使各项完全分离，应该满足下列条件：

而

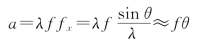
故

应该指出的是，用傅里叶变换匹配滤波手段进行图像的特征识别处理有其局限性。这是因为匹配滤波器对被识别图像的尺寸缩放和方位旋转都极其敏感（其敏感程度取决于它所匹配的图样的结构，一般要求小于10%的尺寸变化和小于5°的转角），因而当输入的待识别图像的尺寸和角度取向稍有偏差或滤波器自身的空间位置稍有偏移时，都会使正确匹配的滤波器产生的响应急剧降低，甚至被噪声所湮没，使识别发生错误。目前，已被采用的一种解决方法是制作一组匹配滤波器，其中每一个滤波器与具有不同转角或尺寸的待检测的图样匹配。若这些匹配滤波器中的任何一个有大输出，就说明待测图样已出现在输入上。

为了更好地解决这一困难，多年来经研究人员的努力，又发明了多种实现特征识别的方法，例如，利用梅林变换解决物体空间尺寸改变的问题；利用圆谐变换（Circular Harmonic Transform）解决物体的转动问题；利用哈夫变换（Hough Transform）实现坐标变换；等等。再结合傅里叶变换匹配滤波操作，使其更完善、更实用。近年来随着空间光调制器的研究进展，各种实时器件开始进入应用阶段，用这些器件代替特征识别系统中的全息匹配滤波器，可实现图像的实时输入、滤波和输出。另一方面是将光学与电子计算机结合，实现数字化和智能化。