信息光学：全息照相法

该方法的特点是采用了一个π相移板，并应用二次曝光法来记录两幅全息图像。其光路如图7.1.2所示。在输入平面P1上放置第1个图像A，在干板架H上放置全息干板，先记录图像A的全息图，然后拿掉A，将图像B置入，并加入一个π移相板使物光位相延迟π，再记录图像B的全息图。这样记录的二次曝光全息图，经显影、定影和反皱缩处理后放回干板架上，当用原参考光照明时，在重现光场中同时包括图像A和B，由于在记录过程中使A和B物光的位相差为π，故重现时二者的相同部分便干涉相消，只留下了差异部分。

图7.1.2　全息法图像相减光路

为了进一步理解用全息法进行图像相减的原理，下面对上述记录过程再进行较详细的分析。设参考光为平面波R（x，y）=e-i2πξx，其中，ξ=，（x，y）为H面上的位置坐标。又设图像A和B在H上的光场分布分别为A（x，y）和B（x，y），则记录A的全息图面上的光强分布为

记录B时物光引入了位相差π，变为Beiπ=-B，故记录面上的光强分布为

两次曝光后的总光强分布为(www.xing528.com)

假设全息底片工作在线性区内，则显影、定影后的全息图的透射率为τ=τ0+βI，式中τ0、β为常数。再现时对全息图进行傅里叶变换，有

其中有一项为

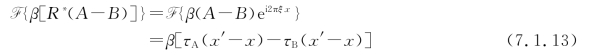
式中，τA、τB分别相应于图像A和B的振幅透过率。式（7.1.13）显然实现了图像A和B的相减，可以在频谱面P2上的确定位置找到相减图像的频谱。