正弦光栅法在信息光学中的应用

此方法的特点是利用正弦振幅光栅作为空间滤波器。设此正弦光栅的空间频率为f0，将其置于4f系统的滤波平面P2上，如图7.1.1所示，光栅的复振幅透过率为

式中，；f为傅里叶变换透镜的焦距；φ0表示光栅条纹的初位相，它决定了光栅相对于坐标原点的位置。

将图像A和图像B置于输入平面P1上，且沿x1方向相对于坐标原点对称放置，图像中心与光轴的距离均为b。选择光栅的频率为f0，使得b=λff0，以保证滤波后在输出平面上两图像中A的+1级像和B的-1级像能恰好在光轴处重合。由于正弦振幅光栅的频谱包括3项（0级、±1级），因此对于一个中心在x1=b的图像，经光栅在频域调制后，可在输出面上得到3个像（0级像位于x3=-b处，±1级像对称分布于两侧）；由于f0受的限制，因而必有+1级像处于输出面的原点处（光轴上），而-1级像的中心在x3=-2b处。同理，对于x1=-b的图像，其在输出面也有3个像（0级像位于x3=b处，而±1级像则分别位于x3=+2b和0处），因此，A的+1级像与B的-1级像在像面原点重合（但需注意：图7.1.1输出面中取的反演坐标系）。于是，输入场分布可写成

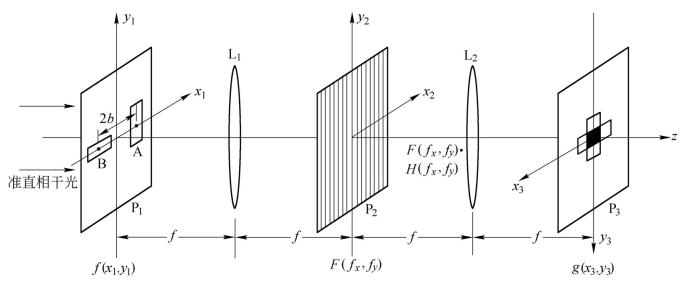
图7.1.1　利用光栅实现图像相减

在其频谱面P2上的频谱为

由于b=λff0及x2=λffx，故有fxb=f0x2。式（7.1.3）遂可写成

经光栅滤波后的频谱为(www.xing528.com)

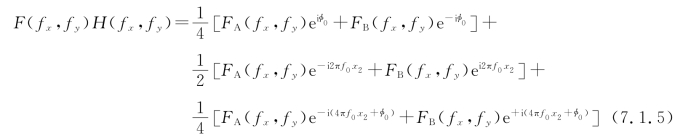
通过透镜L2进行傅里叶逆变换（取反演坐标系统），在输出平面P3上的光场为

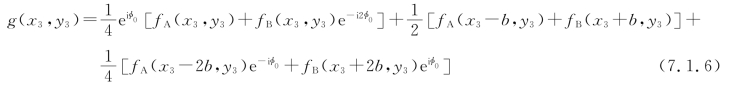
当光栅条纹的初位相φ0=，即光栅条纹偏离纵轴线周期时，式中第1行中的因子e-i2φ0=-1，于是式（7.1.6）变为

结果表明，在输出平面P3上系统的光轴附近，实现了图像相减。

当光栅条纹的初位相φ0=0，即光栅条纹与纵轴线重合时，式（7.1.6）第1行中的指数因子均等于1，结果在输出平面P3上系统的光轴附近实现了图像相加。

从两图像的相加状态转变到相减状态，光栅的横向位移量Δ应等于周期，即满足：

因此，小心缓慢地横向水平移动光栅时，将在输出面P3中心轴线处观察到A、B两图像交替地出现相加和相减的效果。