空间滤波器应用举例-《信息光学理论与应用》

1.泽尼克相衬显微术（Phase-contrast Microscopy）

在显微术中所观察的许多物体（例如，未染色的细菌、生物切片、透明介质等），其透明度很高，几乎不可见。它们通常用折射率的变化来表征。当光通过这样的物体时，即使其各部分存在着厚度的差别，也只能改变入射光的位相，从而产生一个随空间变化的相移，而不改变入射光的振幅。我们把这类物体称为位相物体（Phase Object）。通过普通的显微镜和只对光的强度有响应的感受器是无法直接观察这类物体的。为了观察位相物体，须将其上面的位相变化转换为振幅（强度）变化，这种变换称为相幅变换。下面先介绍由F.Zernike于1935年提出的位相反衬法（简称相衬法）。

设位相物体的复振幅透过率为

式中，φ（x1，y1）是光通过位相物体时所引起的位相变化，并设此物体在成像系统中用相干光照明。为了数学分析上更简单，令成像系统的放大率为1，且忽略其出射光瞳和入射光瞳的有限大小。如果位相变化很小，即≪1 rad，则可将式（6.2.2）展成泰勒级数，而只保留前两项：

其中第1项将带来一个通过物体而不发生变化的强的分量波，第2项则产生较弱的偏离系统光轴的衍射光。当用单位振幅的单色平面光波照明此位相物体时，透过的光场振幅分布为τ（x1，y1）=1+iφ（x1，y1），故一个普通显微镜对上述物体所成的像，其强度可以写成

Zernike指出，衍射光之所以观察不到是由于它与很强的本底之间存在的位相差，如果能够改变直射光与弱衍射光之间的这种位相正交关系，那么两项就会更直接地叠加并发生干涉，产生可观察的强度变化。为此，他提出在频谱面上放置一块变相板（Phase-Changing Plate），以改变被聚焦的本底光和衍射光之间的位相关系，同时使本底光的强度适当衰减。这个变相板通常是通过在优质光学玻璃平板的中心淀积一层透明材料而成，它实际是一个位相滤波器，其滤波函数为

式中，t为本底光（零级频谱）的透过率，且有0＜t＜1。于是，滤波后的频谱为

F{τ(x1,y1)}H(fx,fy)=±itδ(fx,fy)+iΦ(fx,fy)

像面上的复振幅分布为

g(x3,y3)=±it+iφ(x3,y3)=i[±t+φ(x3,y3)]

像面上的强度分布为

于是得到了像面光强分布与物体位相分布之间的线性关系，并使物体位相的变化转换为像强度的变化，从而使位相物体在显微镜下变成可见的。当本底光位相被延迟时，方程（6.2.6）中取正号，则物体位相值大的地方像强度也大，这一结果称为正相衬或亮相衬；当本底光位相被延迟（或-）时，方程（6.2.6）中取负号，则物体位相值大的地方像强度较弱，这一结果称为负相衬或暗相衬。

相衬法是一种将空间位相调制转换成空间强度调制的方法。相衬显微术可用于任何一类φ（x1，y1）≪1的位相物体。当φ变大时，这一技术仍将使位相物体变成可见的，但强度变化不再正比于其位相的变化。目前，相衬显微镜已有定型产品。当然，相衬法不限于显微系统，它适用于任何相干成像系统。

图6.2.4是根据相衬法制成的相衬显微镜的典型光路。L1和L2为聚光镜，在L2前焦面上放置一个环形光阑D1，光源S经L1成像在D1上。D1可看作二级环形光源，它发出的光经L2成平行光倾斜照明位相物体t。在显微物镜L3的后焦面安置移相板D2，其上镀有环形金属膜层，以产生相移和吸收，其位置恰好在直接透射光会聚处，物体产生的衍射光主要从未镀膜处透射，可在像面上观察到弱位相物体产生的光强变化。

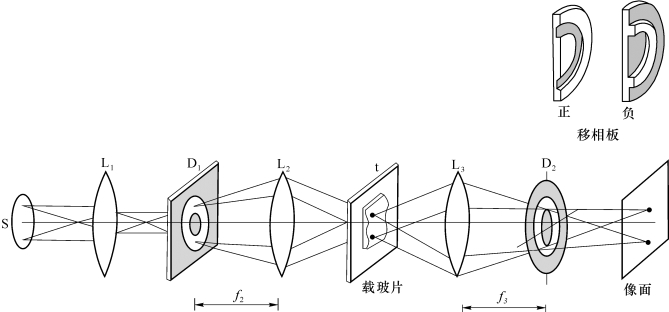
图6.2.4　相衬显微镜的光路（只画出零级光）

泽尼克的成功给了我们重要的启示。光波携带物体信息传播时，信息承载的方式可能是空间的振幅和位相调制、空间强度调制或空间的波长调制，这取决于照明光波的性质以及物体本身的形状、亮暗和色彩等因素。我们不仅可以通过滤波或其他方法就每一种调制方式本身做出各种变化，还可以在信息的不同调制方式之间实现变换，也就是改变编码方法。泽尼克利用位相滤波改变不同频率成分之间的位相关系，使空间位相调制的信息变换为空间强度调制的信息，以便于观测，这就是一个成功的例子。

2.补偿滤波器

提高光学系统的成像质量始终是光学工作者所追求的目标。20世纪50年代初期，在巴黎大学工作的法国科学家马尔查（A.Maréchal）认为，照片中的缺陷是由于产生照片的非相干成像系统的光学传递函数中存在相应缺陷而引起的。他进而推论如果把照相底片放在一个相干光学系统内，并在其频谱平面上放置适当的补偿滤波器，使用该滤波器的传递函数来补偿原系统传递函数的缺陷，则两者的乘积便能产生一个较为满意的频率响应，从而使照片的质量得到部分改善。例如，假定成像缺陷是由成像系统严重离焦引起的，则在几何光学近似下，离焦系统的脉冲响应是一个均匀的圆形光斑，其点扩展函数为

式中，d为圆形光斑的直径。相应的传递函数为

式中，ρ=是极坐标下的空间频率变量。(www.xing528.com)

如图6.2.5（a）所示是补偿滤波器的结构示意，由一块吸收板和一块退相板组合而成，把它安放在4f系统的频谱面上，H（ρ）的函数曲线如图6.2.5（b）所示。从图中明显看出，在未补偿前传递函数的高频损失严重，而且在某一中间频率区间，传递函数的符号发生了反转。补偿滤波器的吸收板使H（ρ）的很强的低频峰发生衰减，以便提高像的对比度，突出细节；而退相板使中间频率区域反转的传递函数相移π。补偿后的传递函数（图中实线）比较均匀，因而明显地改善了成像质量。

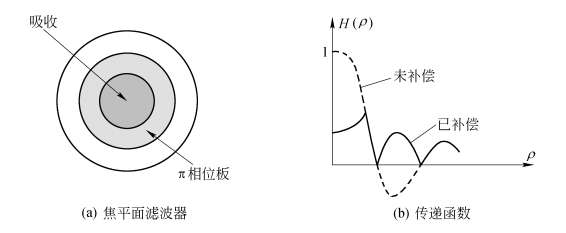
图6.2.5　补偿滤波器

马尔查和他的同事们还研究了衰减物频谱的低频分量，从而找到突出像中微小细节的方法，并用简单的滤波器消除半色调图片上的周期性结构。他们的成就为后来人们对光学信息的处理提供了强有力的推动。

3.抑制或提取周期信息

由于制版和印刷的需要，报纸上的照片是由大量周期排列的黑点组成的。照片的黑白层次由黑点的大小控制（点染制版法）。类似地，电视图像由一系列水平排列的线条（行扫描线）组成。我们把这些不属于图像本身的周期结构叫作“周期性噪声”，应用空间滤波方法很容易把这些噪声去掉。由于这些噪声的周期比较小，对应的空间频率较高，而在频谱面上图像本身的频谱集中在以零频为中心的低频范围，于是，在滤波系统的频谱面上插入一低通滤波器，选择合适的圆孔直径使噪声的频率分量不能通过，便可在像面上得到一幅没有周期性噪声的图像（图6.2.6）。

图6.2.6　抑制或提取周期信息

4.暗场法

暗场法的光路如图6.2.7所示，频谱面上的空间滤波器是玻璃基片上的一个小圆屏（如墨点），调节小圆屏位置使其与透镜L1的后焦点对准，这时经位相物体直接透射的零级谱被全部吸收。零频分量被吸收后，像面上相干叠加场中的复振幅分布随即发生变化，出现了位相物体信息对像面强度的调制。

图6.2.7　暗场法光路

仿前节中相衬法的讨论，设被观察位相物体的复振幅透过率表示为

其中|φ（x1，y1）|≪1 rad。当用单位振幅的单色平面光波垂直照明时，透过该位相物体的光场分布为

其中第1项是直接透射光，它平行于光轴，会聚于透镜L1的后焦点，形成物谱的零频分量，当把一个小圆屏滤波器置于后焦点处时，便会把此直接透射光挡去。式（6.2.10）中的第2项是衍射光，经透镜L1会聚后，主要分布在焦点以外的后焦面上，它不受小圆屏的阻挡。

挡掉零频分量后，像的强度分布变为

式中，M是光学系统放大倍数，x3和y3前面的负号表示成倒像。由式（6.2.11）可见，采用中心暗场法所得到的像的强度变化与位相变化不成线性关系。而一般说来，位相变化是与介质厚度成线性关系的，故用暗场法不能根据强度分布直接测出介质厚度的变化。

另外，在像面上除位相信息之外的其他区域，是物平面上入射光通过的等厚度的透明区域，其主要成分是零频及其附近的低频，几乎全部被滤波器所吸收，形成一片暗场，故称为暗场法。

本章重点

1.空间频谱分析系统。

2.几种典型的空间频率滤波系统。

3.空间滤波的傅里叶分析。

4.空间滤波器结构类型和应用举例。

5.Zernike相衬显微术。