空间滤波的傅里叶分析：信息光学理论与应用最新研究成果

为了进一步理解系统透射频谱对像结构的影响，下面以一维光栅为例，采用傅里叶分析方法来分析空间滤波过程。

根据1.3节和2.5节中的讨论，一维光栅的透过率函数可表示为

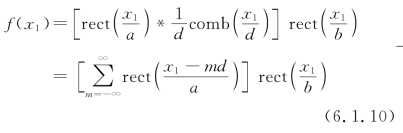
其函数图像如图6.1.8（a）所示。其中a为缝宽，d为光栅常数，b为沿缝宽方向光栅的总宽度。将此光栅置于图6.1.6所示的4f系统的输入平面P1上，则在频谱平面P2上将得到其频谱函数如下：

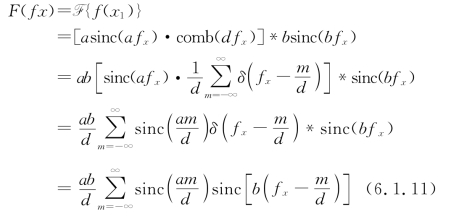
式中，fx=，x2是频谱面P2上的位置坐标。其频谱函数曲线如图6.1.8（b）所示。为了避免各级频谱重叠，以便实现准确滤波，假定b≫d。下面讨论在频谱面P2上放置不同的滤波器时，在4f系统的输出面P3上像场的变化情况。

1.狭缝滤波器只让零级谱通过

狭缝滤波器的透过率函数如图6.1.8（c）所示，它只让式（6.1.11）中m=0的项通过，因而滤波后的频谱函数为

其函数图像如图6.1.8（d）所示。于是，在输出平面上的像场分布〔见图6.1.8（e）〕为

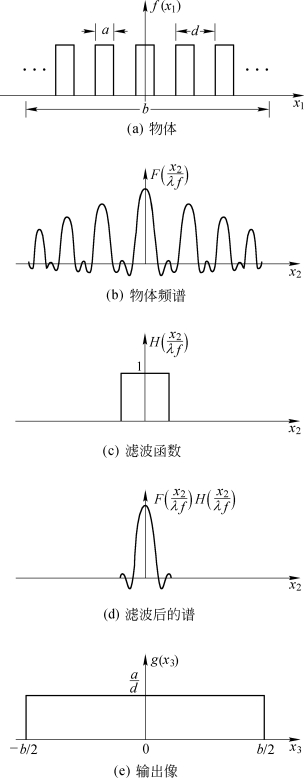
图6.1.8　一维光栅经滤波的像（透过零级）

在像平面上呈现出均匀一片亮，没有强度起伏，也没有周期条纹结构。

2.狭缝增宽到能允许零级和正、负一级通过

整个滤波过程如图6.1.9所示。滤波后的频谱函数为式（6.1.11）中取m=0，±1的前3项，即

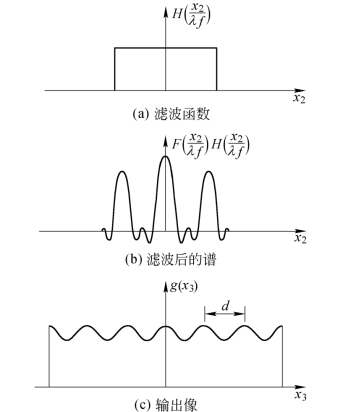
图6.1.9　一维光栅经滤波的像（透过零级和正、负一级频谱）

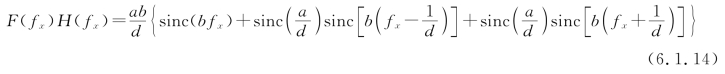
于是，在输出平面上的像场分布为

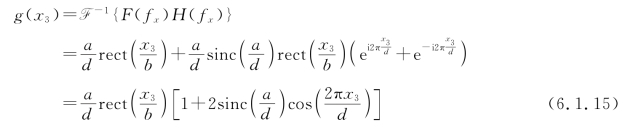
此时，像出现周期性结构，且和物的周期同为d。由于损失了高频信息，像变成了对比度较低的余弦振幅光栅。(www.xing528.com)

3.双缝滤波器仅允许正、负二级频谱通过

双缝滤波器的滤波过程如图6.1.10所示。滤波后的频谱函数为式（6.1.11）中取m=±2的对应项，即

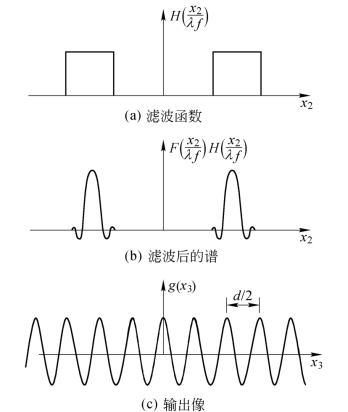
图6.1.10　一维光栅经滤波的像（透过正、负二级频谱）

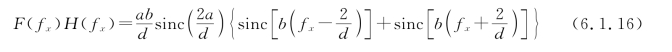
在输出平面上的像场分布为

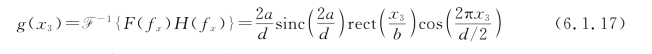
在这种情况下，像的结构是余弦振幅光栅，但其周期为物周期的一半。

4.小圆屏滤波器仅阻挡零级频谱而允许其余频谱全部通过

其滤波过程如图6.1.11和图6.1.12所示。滤波后的频谱函数为

输出平面上的光场分布为

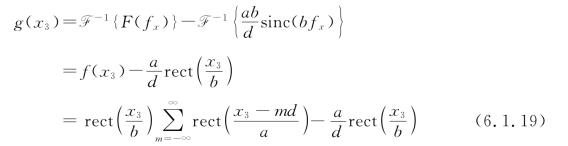
由上述结果可引出两个重要的实验现象：

（1），即狭缝宽度等于两相邻狭缝间不透光部分的宽度。此时，直流分量为，输出面上像场的复振幅仍为光栅结构，且与物周期相同，但强度分布是均匀的，没有起伏，如图6.1.11所示。

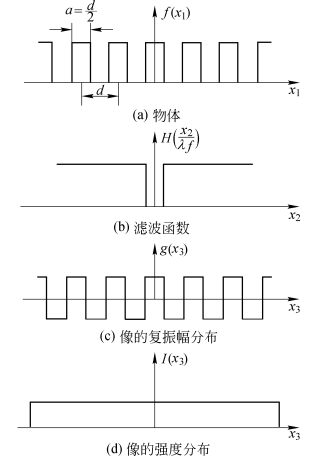
图6.1.11　去掉零频后一维光栅的像（a=）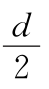

（2），即缝宽大于缝间不透光部分的宽度。此时，由于直流分量大于，故输出面上像场的复振幅分布如图6.1.12（c）所示，从而使像的强度分布呈现对比度反转〔如图6.1.12（d）所示〕，原来的亮区变成了暗区，原来的暗区变成了亮区。

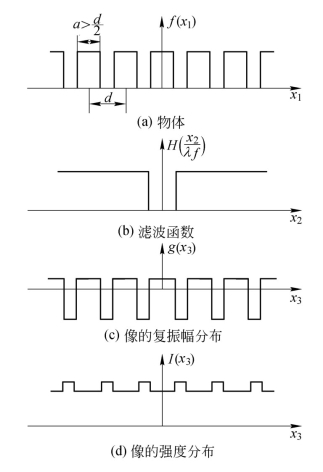
图6.1.12　去掉零频后一维光栅的像（a＞）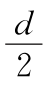

以上对滤波过程所做的傅里叶分析与实验结果完全相符，证明了利用空间滤波技术可以成功地改变像的结构。