信息光学理论与应用：空间频率滤波系统

空间频率滤波系统是相干光学信息处理中一种最简单的处理方式，它利用了透镜的傅里叶变换特性，把透镜作为一个频谱分析仪，并在其频谱面上通过插入适当的滤波器，借以改变物的频谱，从而使物图像得到改善。

空间频率滤波系统有多种光路结构，下面介绍最常用的几种类型。

1.4　f系统

4f系统是最典型的一种相干光学信息处理系统，其光路结构如图6.1.6所示。由相干点源S发出的单色球面波经透镜LC准直为平面波，垂直入射到输入平面（物面）P1上。P2为频谱平面（即滤波面），P3为输出平面（即像面）。L1、L2为一对傅里叶透镜，用来在由P1面至P3面之间进行两次傅里叶变换。P1、L1、P2、L2、P3之间的距离依次均取为透镜的焦距f，故此光路系统常简称为4f系统。

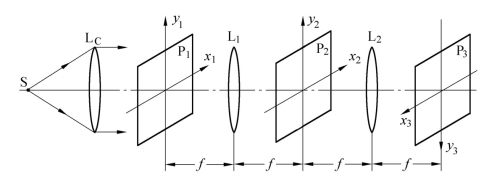
图6.1.6　常用的相干光学处理系统（4f系统）

设输入物的复振幅透过率为g（x1，y1），则它在频谱面上的频谱函数为

G(fx,fy)=F{g(x1,y1)}

如果在频谱面上插入一个滤波器，其复振幅透过率（或称滤波函数）为

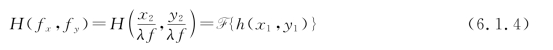
式中，h（x1，y1）称为滤波器的脉冲响应函数，则透过滤波器的光场复振幅分布为G（fx，fy）H（fx，fy），再经过透镜L2作第二次傅里叶变换，在输出平面P3上产生光场复振幅分布g（x3，y3）。在反射坐标中可表示为

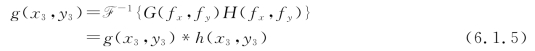
于是在此情况下，4f系统执行的是函数g与函数h的卷积运算。其输出光强度分布可表示为

(www.xing528.com)

如果在频谱面上插入滤波器，其复振幅透过率为

则在输出平面上得到的复振幅分布为

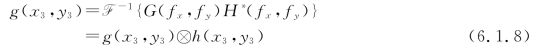
这时，4f系统执行的是函数g与函数h的相关运算。其输出光强度分布为

由上述讨论知：从频域来看，改变滤波器的透过率函数（滤波函数），该系统就能改变物图像的空间频谱结构，这就是空间滤波或频域综合的含义；从空域来看，系统实现了输入信息与滤波器脉冲响应的卷积或相关，完成了所期望的一种变换。

2.其他典型的滤波系统

如图6.1.7所示为另外3种典型的滤波系统。其中图6.1.7（a）是一种双透镜系统，L1是准直透镜，L2同时起傅里叶变换和成像作用，频谱面在L2的后焦面上，输出平面P3位于P1面的共轭像面处。图6.1.7（b）是另一种双透镜系统，L1既是照明透镜又是傅里叶变换透镜，照明光源S与频谱面是物像共轭面，L2则起第二次傅里叶变换和成像作用。图6.1.7（c）是单透镜系统，L具有傅里叶变换和成像双重功能，照明光源S与频谱面共轭，物面与像面形成另一对共轭面。

图6.1.7　其他3种典型的滤波系统

在图6.1.7（b）、（c）两种滤波系统中，前后移动物面P1的位置，可以改变输入频谱的比例大小，这种灵活性给滤波操作带来了方便。这3种滤波系统结构简单，但是这3种系统在P2面上给出的物频谱都不是物函数准确的傅里叶变换，而附带有球面位相因子，这在某些运用中将对滤波操作带来影响。此外，由透镜孔径（如L2）所产生的渐晕效应较大，也是需要注意的。对于4f系统，由于变换透镜的前后焦面上存在准确的傅里叶变换关系，分析起来十分方便，故在一般的光学信息处理系统中（如匹配滤波、图像消模糊等）都采用4f系统，只有在光学成像系统中才用到图6.1.7的光路。