全息光学元件应用指南

所谓全息光学元件（HOE）是指用全息照相方法（包括计算全息法）制作的，可以完成准直、聚焦、分束、成像、光束偏转和光束扫描等功能的元件。在完成上述功能时，它不基于光的反射和折射规律（几何光学），而基于光的干涉和衍射原理（物理光学）。因此，也把它称为衍射光学元件。最常用的全息光学元件是全息光栅和全息透镜。

1.全息光栅（Holographic Grating）

传统的刻痕光栅是在一块经过精加工的光学玻璃平板上，通过刻划机的刻刀一道一道刻出许多等宽、等间距的平行刻痕而成。先制成母光栅，再进行复制。在每条刻痕处，入射光向各个方向散射，而不易透过；两刻痕之间的光滑部分可以透光，与缝相当。这种光栅属于振幅型透射光栅。由于光栅的刻痕密度很高，每毫米内刻痕数通常在数十条至数千条之间，而在刻划母光栅时，其刻划动作又十分缓慢（每分钟仅刻6条线），因此，即使刻一块长宽都为5 cm的光栅，以每毫米刻1 200条计，并且令刻划机昼夜不停工作，也需要运行一周。这对刻划机的工作条件（环境温度变化不得超过0.1℃）和机械结构（刻划分度的均匀性）都提出了极苛刻的要求。例如，当推动光栅坯子的螺纹有周期性误差（机械本身精度的限制）时，将引起刻痕光栅条纹的不均匀性，从而在光栅光谱线的主极大两旁对称地产生两条弱线，称为罗兰鬼线（Rowland Ghost），它直接影响了光谱分析。上述原因导致传统刻痕光栅价格较昂贵，且刻划面积不可能很大。

全息光栅克服了刻痕光栅的上述缺点。其记录光路如图5.9.3所示，采用两束平行光记录。根据5.7节的讨论，并结合图5.9.3，可将式（5.7.10）改写成

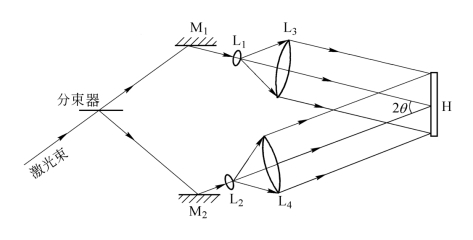
图5.9.3　全息光栅记录光路

式中，θ为两平行光束夹角之半。上式称为光栅方程。由该式可知，改变两束光之间夹角2θ的值便可控制光栅条纹密度（即d的大小）。全息光栅与刻痕光栅相比，具有下列优点：光谱中无鬼线、分辨率高、有效孔径大、生产效率高、价格便宜等。缺点是衍射效率较低，应继续设法加以提高。为此，近年来又采用反应离子束刻蚀技术研制了全息闪耀光栅，其一级衍射效率可达60%以上。

2.全息透镜（Holographic Lens）

（1）点源全息透镜

最早的衍射成像元件是1871年由瑞利制成的菲涅耳波带片（Fresnel’s Zone Plates）。当时因其衍射效率低和多级像的存在，而没有得到实际应用。但自20世纪60年代激光器和全息术发展起来以后，人们意识到可以用点源全息图来制作波带片。这就促使其发展成另一类光学成像元件——全息透镜。

点源全息透镜的一种制作光路如图5.9.4所示，采用一发散球面波与一固定的会聚球面波相干涉。根据记录介质表面中心的法线与R、O两点源的连线是否重合，可分为同轴全息透镜与离轴全息透镜；根据R、O两点源处于全息干板的两侧或同侧，又分为反射式全息透镜与透射式全息透镜。图5.9.5是离轴全息透镜的两种记录方式。按照需要并选择适当的光波波面，可制成准直透镜、成像和转像透镜、傅里叶变换透镜以及多功能透镜（可代替组合透镜）等。由5.2节的讨论及式（5.2.9a）知，在图5.8.4所用符号下有

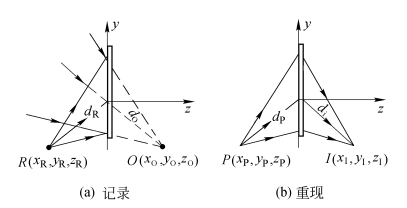
图5.9.4　点源全息透镜

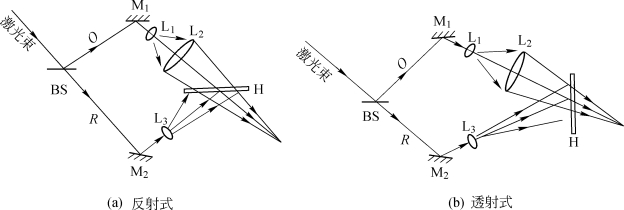
图5.9.5　离轴全息透镜记录光路

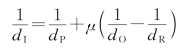(www.xing528.com)

或

上式就是全息透镜近轴像点的高斯公式，f′是透镜的焦距。

理论分析表明，在近轴条件下，全息透镜与普通透镜的几何光学分析具有惊人的一致性。它可以按照与折射透镜类似的方法来定义光轴、主轴、物平面、像平面、焦距、孔径光阑和相对孔径等概念，并满足普通透镜的物像公式。进一步的研究表明，全息透镜可以用一个折射率趋于无限大的等效折射透镜来精确模拟。采用等效透镜的概念后，全息光学系统也可以应用普通光学系统的计算机程序来进行优化设计。

和普通透镜相比较，全息透镜具有重量轻、造价低、相对孔径大，易于制作和批量复制等优点，并能做成透射式、反射式和折叠式光路，在同一张全息片上可具有多功能（如聚焦、分束、滤波和多重记录），它已在许多领域获得了应用。全息透镜的缺点是像差较普通透镜大，尤其是色差。这是因为全息透镜是一种衍射元件，其成像特性与光波波长有关，故色差更为严重。单片的全息透镜只能在单色光条件下工作，将两片以上分离的全息透镜组合起来便可校正色差，也可使其在宽带光源照明条件下工作。

全息透镜的单色像差不能像普通透镜那样，通过选择不同性能的玻璃材料、改变透镜表面曲率半径或形状、调整透镜间距或光阑位置来校正，但可通过计算，把像面上的像差转移到记录波面上去（计算全息），亦即可用带有适当像差的变形波面与理想球面波干涉，以综合出一个无像差的全息透镜。图5.9.6给出了一个这样的记录光路，精心设计的计算机原生全息图（Computer Generated Hologram，CGH）产生需要的像差波面A，然后平面波B与变形波面A干涉，综合出一个无像差的全息透镜。这种方法已经在全息透镜的设计制造中得到了广泛的应用。

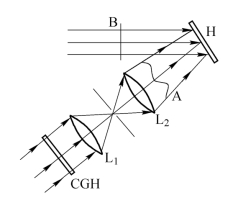
图5.9.6　无像差全息透镜的记录光路

（2）全息透镜阵列

在实际工作中，常常需要把若干个全息透镜记录在同一张干板上，并按一定顺序排列，形成全息透镜阵列（Holographic Lens Array）。这种全息透镜阵列在光互连、光学神经网络和光计算中都有很高的应用价值。图5.9.7是制作同轴透射式全息透镜阵列的光路，采用两个相同的物镜L1、L2产生两个孔径相同的会聚球面波，适当安排L1、L2的位置，使光通过分光镜BS2后产生一前一后两个焦点。在两个焦点的中间位置安放全息干板即可记录同轴全息透镜。把干板放置在可沿x、y方向移动的干板架上，则经每次移动，分次曝光，即可得到同轴全息透镜阵列。

假设L1、L2的相对孔径为，全息透镜的相对孔径为，前后两焦点之间的距离为lf，则由图5.9.7的几何结构很容易推知，而lf=4fH（在一前一后两焦点之间满足物像关系），故有

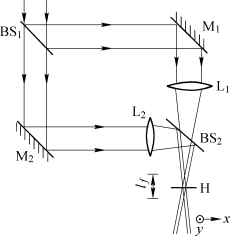
图5.9.7　小孔径同轴全息透镜记录光路

由此可见，只要适当调节L1、L2的相对位置，就可以得到口径非常小的同轴全息透镜，而且不管其口径多小，同轴全息透镜的相对孔径总是所用物镜相对孔径的两倍。