透射体积全息图在信息光学中的应用

为简单起见，设物光波与参考光波均为平面波，其传播矢量均位于xOz平面内，如图5.7.1所示。合光场的复振幅分布为

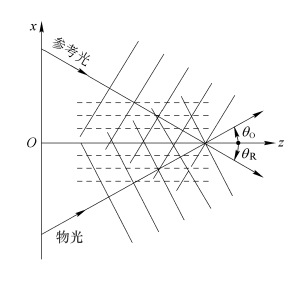
图5.7.1　透射体积全息图的记录

式中

θ0和θR分别为物光与参考光在记录介质内的传播矢量与z轴的夹角，λ为在记录介质内光波的波长。合光场强度的空间分布为

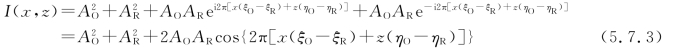
在线性记录条件下，记录介质内振幅透过率的空间分布为

注意到β＜0，则τ（x，y，z）取极小值与极大值的条件分别为

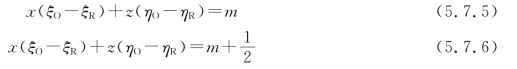
式中，m=0，±1，±2，…。上述两个方程各自确定一组与xOz平面垂直（与y轴平行）的彼此平行的等距平面，即形成体光栅。对于τ（x，y，z）取极大值的平面，显影时乳胶析出的银原子数目也最少。这些平面相对于z轴的倾角φ为

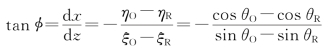
再应用三角公式：

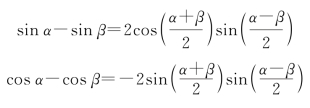(www.xing528.com)

最后得到

于是，在乳胶层内，τ（x，y，z）相等的平面平分物光波与参考光波传播方向所构成的夹角，形成一组垂直于xOz平面的体积光栅。当物光束与参考光束相对于z轴对称时，θR=-θO，从而ξR=-ξO，ηR=ηO，光栅平面方程变为

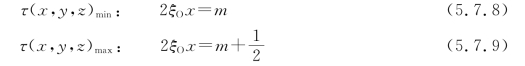
且光栅平面垂直于x轴，光栅间距d为

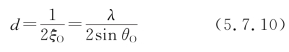
重现时用平行光波照明全息图片，将体积光栅中的每个银层看作是一面具有一定反射能力的平面反射镜，它按反射定律把一部分入射的光能量反射回银层同一侧，如图5.7.2所示。

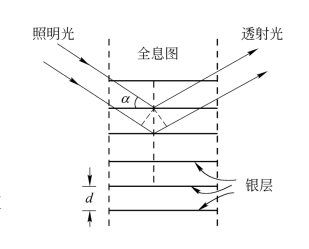
图5.7.2　透射体积全息图的重现

体积全息图对光的衍射作用与布拉格对晶体的X射线衍射现象所做的解释十分相似。设照明光波的传播方向与银层平面的夹角为α，则相邻银层平面反射的光波之间的光程差为ΔL=2d sinα，显然，只有ΔL为重现光波长的整数倍时，各层面反射的光波才能同位相地相干叠加，从而产生一个明亮的重现像，可见其条件是

公式（5.7.11）称为布拉格条件（Bragg Condition）。与式（5.7.10）对比可知，只有在

时才能得到明亮的重现像。上式表明：当用原参考光或与原参考光反向的共轭光照明体积全息图时，将分别重现出原始物波和它的共轭光波，前者给出物体的虚像，后者给出物体的实像。顺便指出，常用的全息干板，其乳胶层厚度约在10μm（见表5.3.3），全息图中形成的条纹根据物、参光波之间夹角的不同，其宽度只有几个光波波长，有时小到半个波长，因而全息图将至少包含一些展现出厚光栅性质的条纹，即在大多数情况下都必须考虑布拉格衍射效应。当用白光照明重现时，改变照明光入射角度，只能在某一小角度范围内观察到重现像。透射体积全息图这种对角度敏感的特性使其可用于全息多重记录和高密度信息存储，此时只需每记录一次后适当改变参考光的方向即可。