信息光学理论与应用：无透镜傅里叶变换全息图

无透镜傅里叶变换全息图（Lensless FTH）应用了菲涅耳衍射与傅里叶变换之间的关系，记录光路如图5.5.4所示。用平行光照明物体，物体与参考点源位于同一平面内，在距离z处放置记录介质。根据菲涅耳衍射的傅里叶变换表达式（2.4.11），在全息底片平面上的物光分布可以写成

图5.5.4　无透镜傅里叶变换全息图记录光路

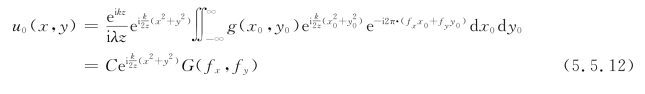
式中

参考光在全息底片平面上的光场可写成

忽略其中的常位相因子，可写成

从而在记录平面上，物光与参考光叠加后所产生的曝光强度为

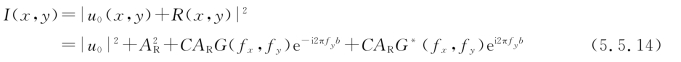
由于物光与参考光中的二次位相因子在曝光强度表达式中相互抵消，故在上式中已不再有与x、y有关的二次位相因子。这就是可以省去透镜记录傅里叶变换全息图的原因。

无透镜傅里叶变换全息图可以用发散球面波重现，也可以用会聚球面波重现。当用发散球面波照明重现时，设光源与全息图的距离为zP，则由式（5.5.12）和式（5.5.14）知，代表原始像的项为

上式与式（5.5.12）相比较，除少一个位相倾斜因子外，还多一个位相因子exp，把它与薄透镜的透过率公式（3.1.4）相比较，可以看出这后一位相因子的作用相当于一个焦距为f的透镜，并满足关系式：(www.xing528.com)

其放大率为M=。因为z和zP均为负值，故根据z和zP的关系可决定重现像的大小如下：

①当z＞zP时，M＞1，f＜0，可得到放大的虚像；

②当z＜zP时，M＜1，f＞0，可得到缩小的虚像；

③当z=zP时，M=1，f=∞，像与物大小相同，在点（0，b）处得到一个原始像，是正立虚像。如图5.5.5所示。

图5.5.5　无透镜傅里叶变换全息图重现光路之一

与共轭像有关的第4项为

类似于对式（5.5.15）的分析可知，在与原始像对称的点（0，-b）处可得一共轭像，是倒立虚像。其放大率M与分析原始像的规律相同，取决于zP与z的关系。

当用会聚球面波重现时，如图5.5.6所示，全息图置于透镜后方，用平行光照明，透镜的作用是对衍射光进行一次傅里叶变换，使在透镜的后焦面上产生两个实像，对称地位于透镜焦点两侧。

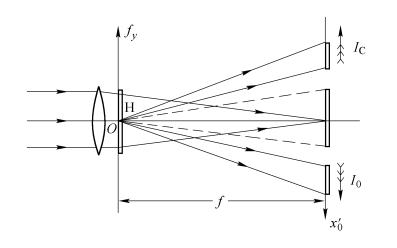
图5.5.6　无透镜傅里叶变换全息图重现光路之二

傅里叶变换全息图在信息的高密度存储、空间频率滤波以及各种光学信息处理系统中有着重要的应用。