全息记录介质的特性评述

1.灵敏度（Sensitivity）

灵敏度是指记录介质在接受光的作用后发生反应的灵敏程度，通常用曝光量的倒数来标志记录介质的灵敏度。底片感光过程是一种光化学作用，光子的能量与波长有关，波长越长，光子的能量越小。因此，每一种记录介质都有一个波长的红限，波长大于红限的光对该记录介质不能起光化学作用。另外，每一种记录介质都有它自己的吸收带，只有在吸收带内的波长方能起光化学作用。这就是各种记录介质对光谱灵敏度不同的原因。

2.衍射效率（Diffraction Efficiency）

衍射效率η定义为全息图衍射成像的光通量与重现用照明光的总光通量之比。衍射效率不仅与记录介质性质有关，还与全息图的类型及条纹的对比度（或调制度）有关。条纹对比度则与物、参光束比有关。由式（4.2.19）知，若令I1=IO，I2=IR，则条纹对比度可写成

由激光器工作原理知道，|γ12（τ0）|是物、参光束光程差（L=cτ0）的周期函数，当L=0时，|γ12（0）|=1，此后每当L为激光器腔长的偶数倍时，|γ12（τ0）|都有一个逐渐减小且小于1的极大值，随着L的增加，最后当|γ12（τ0）|=0.707时，对应的L称为激光束的相干长度。

由式（5.3.4）看出，当IO=IR时V最大，这时Vmax=|γ12（τ0）|，如果此时物光与参考光的光程相等，则|γ12|=1，从而有最大的条纹对比度。但在进行全息照相时，由于种种因素的限制，是不可能做到这一点的。此外，虽然在IO=IR时V最大，这时的衍射效率也可达到最大，但因物光常伴有散斑噪声（空间位相噪声）和调制噪声，后者是由每对物点的发光在记录底片上所形成的有害的干涉条纹。故常采用降低物光与参考光光强之比的办法来提高信噪比，这里是以牺牲衍射效率为代价的。一般来说，位相型记录介质的衍射效率比振幅型记录介质的衍射效率高。

表示衍射效率的公式分为两类：一类是平面（薄）全息图，另一类是体积（厚）全息图。下面仅讨论平面全息图的衍射效率，它又分为振幅型和位相型两种。

（1）振幅型全息图的衍射效率

正弦振幅型全息图的透射率可表示成

式中，τ0是平均透射率；τ1是调制幅度，与记录全息图时物、参光束比以及记录介质的调制传递函数有关。在理想的最佳条件下，应有。假设重现时用振幅为A的平面光波照明，则重现的±1级衍射光的振幅为，故得最佳衍射效率为

式中，Σ为全息图的面积。

对于非正弦型振幅全息图（设为周期光栅结构），其透射率可表示成

在最佳情况下可设其为罗奇光栅（见图5.3.1），其透射率函数可表示成

图5.3.1　罗奇光栅示意图

式中，d为罗奇光栅周期。上式可展成傅里叶级数：

式中，f0=；各傅里叶系数由下列公式给出

将上列结果代入式（5.3.9），最后得

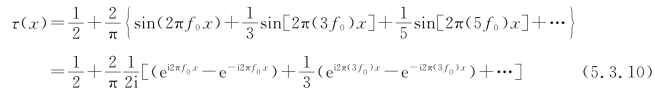
将上式与式（5.3.7）对照可知有，此时±1级衍射光的振幅为，故最佳衍射效率为

由此可见，改变透射函数（即透射波的波形）可适当提高衍射效率。

（2）位相型全息图的衍射效率

正弦型位相全息图的透射率可表示成

其中，φ1为调制幅度。利用贝塞尔函数恒等式

τ（x）可以写成

则第n级的衍射效率为(www.xing528.com)

我们感兴趣的是±1级衍射。注意到φ1=1.85时，J1（φ1）有最大值（见图5.3.2）。此时J1（1.85）=0.582，故得η=ηmax=（0.582）2=33.9%。这时零级和其他各衍射级的衍射效率都小于±1级。由此可见，位相型全息图的衍射效率比振幅型全息图的高得多。

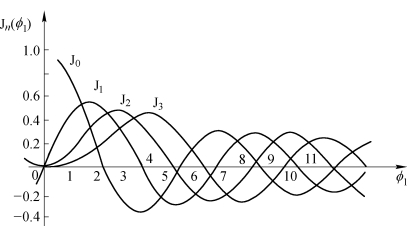
图5.3.2　Jn（φ1）曲线

对于非正弦型位相全息图，在最佳情况下可设其为矩形波位相全息图。此时式（5.3.12）中的φ（x）可以写成〔见图5.3.3（a）〕：

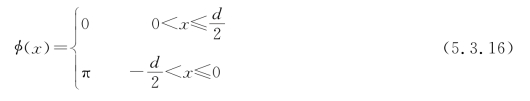
式中，d为全息图光栅间距。上式等效于透射率为

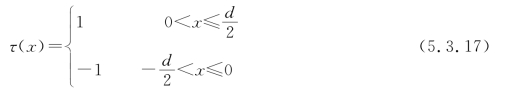
的周期性结构的振幅型全息图〔见图5.3.3（b）〕。将上式展成傅里叶级数式（5.3.9），容易求得各相应的傅里叶系数为

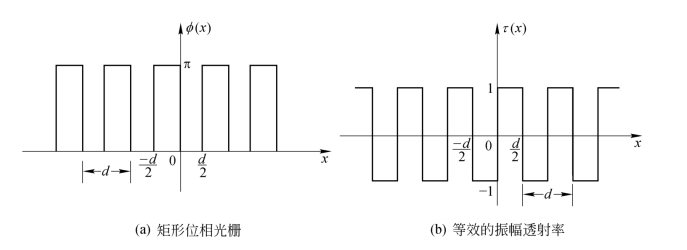
图5.3.3　矩形位相光栅及其等效的振幅透射率曲线

故得

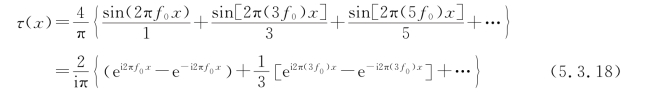
因此，±1级的最大衍射效率为

还要指出，从傅里叶系数表达式可以看出：这种矩形波位相全息图没有零级和偶数级衍射，且其±1级衍射光包含了80%以上的入射光能。

总之，无论是振幅型全息图还是位相型全息图，矩形函数形式的衍射效率都比正弦型的衍射效率高。

表5.3.1列出了各种全息图衍射效率的理论值，以供比较、参考。其中关于体积全息图的衍射效率，可参考文献[6]。

表5.3.1　各种全息图衍射效率的理论值

3.分辨率（Resolution）

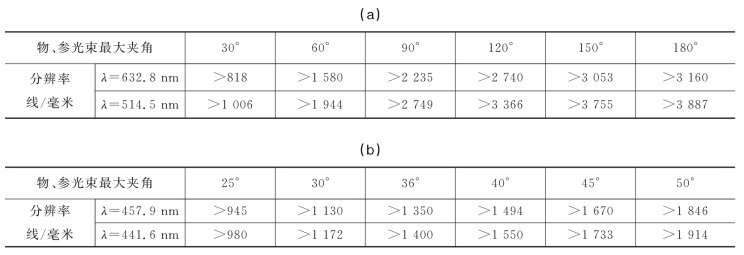
记录介质的分辨率是指它在曝光时所能记录的最高空间频率，其单位是线/毫米。记录介质的颗粒越细，则其分辨率越高，衍射效率也越高，噪声越小，但其灵敏度变低。普通照相底片的分辨率大约为200线/毫米；对于全息底片而言，因为记录的是物光波与参考光波的干涉条纹，故对分辨率要求较高。卤化银超细微颗粒全息底片的分辨率高达3 000线/毫米，甚至更高。例如，美国依尔福（Ilford）公司生产的一种超微粒卤化银乳胶全息底片，其分辨率高达7 000线/毫米（见表5.3.3）。

记录全息图时对底片分辨率的要求与物、参光束间的夹角有关。这可由全息图所形成的条纹光栅满足的关系式（5.7.10）导出

式中，θ为物、参光束间的夹角。表5.3.2给出用对称光路记录透射全息图时，物、参光束间最大夹角对记录介质分辨率的要求。

表5.3.2　透射全息图对记录介质分辨率的要求

4.特性曲线（Characteristic Curve）

人们常用两条曲线来表明全息底片的特性，一条是D-lg E曲线（或称H-D曲线），表示光密度与曝光量对数之间的关系，如图5.3.4所示。其中AB段称为线性曝光区，是通常应用的工作区；BC称为灰雾区段，表示曝光量不足；AD段是过度曝光区段。线性曝光区的斜率γ称为底片的反差系数（Contrast Coefficient），即γ=tanα=，ΔlgE表示线性工作区范围，称为宽容度（Tolerance）。γ值大，表示当曝光量有较小改变时，就可以引起光密度较大的改变，这种底片称为高反差底片（High-Contrast Film，通常γ=2～3）；γ值小则表示与上述情况相反，相应的底片称为低反差底片（Low-Contrast Film，通常γ≤1）。值得注意的是，底片的特性曲线是要在显影、定影等化学处理后才能最后形成的，所以，一张经曝光、显影和定影处理的底片，其实际的γ值不仅与乳胶类型有关，还与显影液的配方和显影时间有关。对全息照相来讲，希望底片的宽容度要大，γ值也要大，灰雾值要小。当然还得考虑具体情况。

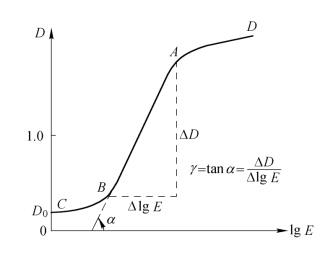
图5.3.4　D-lg E曲线

另一条用来描述全息底片特性的曲线是τ-E曲线，如图5.3.5所示，其中横轴代表曝光量，纵轴代表振幅透过率，曲线中央部分代表底片的线性工作区。从图中看出，底片的反差越高，曲线越陡。

图5.3.5　底片的τ-E曲线