信息光学特殊情况分析

（1）重现光波与参考光波完全一样，即xP=xR，yP=yR，zP=zR，λ1=λ2。这时，由式（5.2.10）得

上式表明，分量波A3产生物点的一个虚像，像点的位置与物点重合，横向放大率为1，它是原物点准确的重现。分量波A4可产生物点的实像或虚像，取决于zi2的正负。当zR＜2zO时，zi2＞0，它产生虚像；当zR＞2zO时，zi2＜0，它产生实像。在通常情况下，此像的横向放大率不等于1。

（2）重现光波与参考光波共轭，即xP=xR，yP=yR，zP=-zR，λ1=λ2。这时由式（5.2.10）得

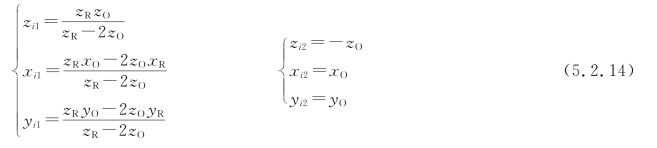
上式表明，分量波A4产生点物的一个实像，且点像与点物的空间位置相对于全息图呈镜面对称。因此，观察者看到的是一个与原物形状相同，但凹凸互易的赝视像。分量波A3可以产生点物的虚像或实像，这取决于zi1的正负。

（3）参考光波与重现光波都是沿z轴传播的完全一样的平面波，即xP=xR=0，yP=yR=0，zP=zR=∞，λ1=λ2，则有

由此可见，此时得到的两个像点位于全息图片两侧的对称位置，一个是虚像，一个是实像。

（4）物点与参考点源都位于z轴上，即xO=xR=0，yO=yR=0。这时，在线性记录条件下，与式（5.2.3）、（5.2.4）相对应的两个透射率分量是

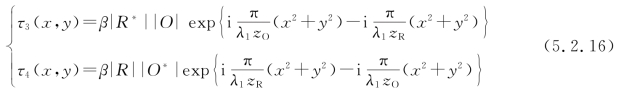
这时干涉条纹是一簇同心圆，圆心位于原点，称为同轴全息图。同轴全息图的重现可以分为两种情况。

①用轴上照明光源重现，xP=yP=0。这时像点的坐标是(www.xing528.com)

这表明两个重现像均位于z轴上。当照明光源与参考光源完全相同时，zP=zR，λ1=λ2，则

这表明分量波A3产生的虚像，与轴上原始物点完全重合。另一个像点的虚实由zi2的符号决定。当照明光源与参考光源共轭时，有

这表明分量波A4产生一个与原始物点位置对称的实像。另一个像点的虚实仍由zi1的符号决定。

②用轴外照明光源重现。这时，像点坐标是

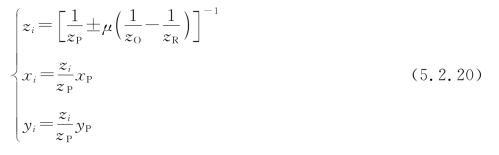
由于，故重现的两个像点位于通过全息图片原点的倾斜直线上。这表明：即使用轴外照明光源重现，同轴全息图产生的两个像仍然沿同一方位，观察时互相干扰，如图5.2.4所示。

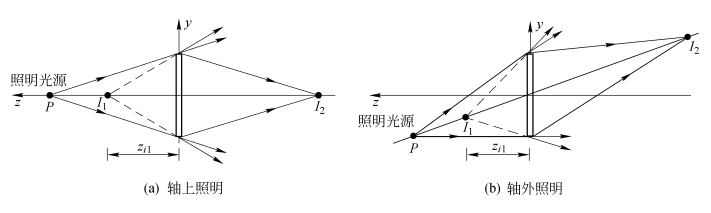
图5.2.4　点源同轴全息图的重现