前面曾经指出，在单色波场中，由于频率恒定，对时间的函数关系已预先知道，故光场的分布可由其复振幅分布完备地描述，它是空间任意点坐标的函数。而在非单色波场中，空间任一点的光扰动随时间做无规则变化，这时需要关注的是光场的统计性质。应在时间-空间坐标系中考察两个不同点的光扰动的关联程度。因而互相干函数是描述光场性质的基本参量。光场中的不同位置，互相干函数是不同的。从这个意义上讲，光波在传播过程中，光场的相干性亦随之传播。
为了找到描述互相干函数传播的方程，按照前节的讨论，首先假定光辐射场可以用一个满足标量波动方程的复标量函数u（r，t）来表示。为了书写方便，略去空间变量，写成
由互相干函数定义：
在上式两端对P1点坐标取拉普拉斯算符，则
由式（4.3.15）可得
假设所考虑的光场是平稳、各向同性的，则可认为式（4.3.18）中对时间t+τ的微分可用对τ的微分代替：
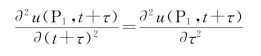
故式（4.3.18）可写为
光辐射场u（P2，t）与τ无关，因此可以对上式中时间平均函数整体取二阶偏导数，得
即
上式可以看成是描述互相干函数传播的基本方程。
同样，在式（4.3.16）两端对P2点的坐标取拉普拉斯算符，可得
公式（4.3.20）、（4.3.21）中的每一个方程描写其中一点（P1或P2）固定，而另一点和参量τ改变时互相干函数的变化。因此，正如前面指出的，光场的相干性包括时间相干性和空间相干性。互相干函数Γ12（τ）满足的波动方程把时间效应和空间效应联系在一起。一般情况下，不可能把时间相干性和空间相干性分离开来。但对准单色光波场，问题却变得简单了，可以单独研究空间相干性的传播。
在准单色条件下，由式（4.3.7）有
J12与变量τ无关，故利用式（4.3.7）和式（4.3.20）、（4.3.21），可得到互强度传播所满足的两个亥姆霍兹方程：
它们是准单色光场中用来描述空间相干性传播的基本规律。
如图4.3.2所示，假定在准单色光波传播的路径中曲面∑1上所有各对点的互强度Γ（P1，P2；τ）为已知，要确定在经过传播后光波照明的任一曲面∑2上的所有各对点的互强度Γ（Q1，Q2；τ）。对方程（4.3.22）求解，将给出所需的关系式。但是以惠更斯-菲涅耳原理为基础进行推导是一种更简单的方法。
图4.3.2 互强度的传播
因非单色场可看作单色扰动的线性组合，而对每一频率为ν的单色光，可表示为u（P，t，ν）=u（P，ν）e-i2πνt。它从∑1面传播到∑2面的规律满足惠更斯-菲涅耳原理，即
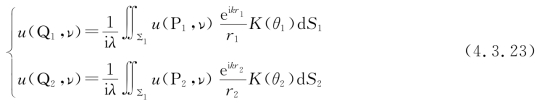
式中，K（θ）是倾斜因子。故对多色光场，u（Q1，t）不妨写成
在准单色光条件下有Δν≪ν0，式（4.3.24）可近似表示为
同样的，有
在∑2面上的互相干函数为
将式（4.3.25）、式（4.3.26）代入式（4.3.27），有
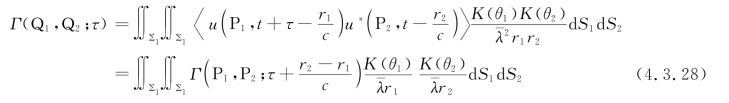
在准单色光条件下，互相干函数可以用互强度表示。由式（4.3.7）有
代入式（4.3.28）可得
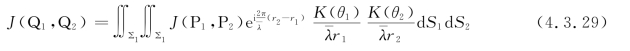
上式就是在自由空间准单色场中互强度的传播公式。若令
式中，k0=
是平均波数，则
公式（4.3.29）和式（4.3.32）表明，传播现象可以看作一个线性系统，满足叠加原理的物理量是互强度，每一对点互强度的响应函数是h（Q1，P1，ν0）h*（Q2，P2，ν0），由式（4.3.31）给出。以J（P1，P2）为权重因子的所有响应函数线性叠加就可以得到∑2面上的互强度。因此，不必要了解光源的具体性质，只要知道输入面上光扰动的相干性，就可以确定输出面上的相干性。换言之，只要知道了点P1和点P2处产生的干涉条纹的对比度，就能确定点Q1和点Q2处产生的干涉条纹的对比度。
当点Q1和点Q2重合为一点Q时，可得到∑2面上的光强分布为
令I（P1）和I（P2）分别表示P1点和P2点的光强度，即(www.xing528.com)
I(P1)=Γ11(0)=〈u(P1,t)u*(P1,t)〉
I(P2)=Γ22(0)=〈u(P2,t)u*(P2,t)〉
则J（P1，P2）可表示成
J(P1,P2)=[I(P1)I(P2)]1/2μ(P1,P2)
式中，μ（P1，P2）表示复空间相干度。式（4.3.33）遂可改写成
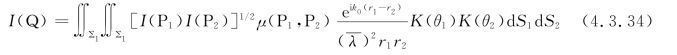
上式，表示Q点的光强等于∑1面上每一对点所作的贡献之和（如图4.3.3所示）。每一对点产生的响应为
K（θ1）K（θ2），每一对点的贡献依赖于这两点的光强以及相应的复空间相干度μ（P1，P2）。式（4.3.34）可以看作是部分相干场中强度传播的惠更斯-菲涅耳原理。它与用于描述单色光波场传播的较初等的惠更斯-菲涅耳公式是极为相似的，其原因是互强度的传播也遵循亥姆霍兹方程。
图4.3.3 计算Σ2上强度I（Q）时的图示
讨论自由空间中准单色场互相干性传播的另一个重要结论是，当对于所有的P1≠P2和所有的τ都有Γ（P1，P2；τ）=0时，式（4.3.28）的积分为零。这就意味着，按照这样的方式定义的非相干场是不能传播的。也就是说，完全不相干的波面是不能辐射的。可以证明，对于一个传播的波，其相干性至少在一个波长的线度上存在。但是对于一般的光学系统，波长相对于波面的尺度可以看作是无穷小量。因此，非相干场的互强度通常近似表示为
式中，（x1，y1）和（x2，y2）分别是P1、P2点的坐标；ρ为一个适当的常系数。
下面举几个计算示例。
【例1】讨论中心频率为ν1和ν2的两个准单色光束间的干涉。计算每个光源的最大容许半宽度值，以及为了探测光拍频的频率差。
【解】设u1（t）和u2（t）是t时刻两个光束在同一点上的场，即
因为假设光场是准单色的，所以u01、u02、φ1和φ2是时间的缓变函数。在任何时刻t的总振幅可以写成
令T0表示探测器的积分时间，则观察到的平均强度为
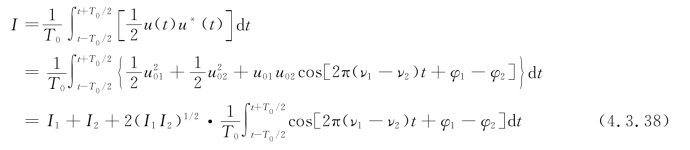
式中，
和
是任一光束在另一光束不存在时的光强度。
当T0远大于任一光束的相干时间时，φ1-φ2在这段时间内的变化是随机的，因此式（4.3.38）中的积分将为零。在此情况下，I=I1+I2，即两光束非相干地相加。
当T0远小于两光束的相干时间（即
），且（ν1-ν2）T0≪1（即两光束的频率差远小于探测器积分时间的倒数）时，在探测时间内，被积函数中的余弦因子可以假设为常数，遂得
因而，探测器将记录下光拍频。使用两个独立的激光束确实可以观察到这种光拍频。另一方面，如果（ν1-ν2）T0≫1，则探测器将再次记录下两束光的强度之和。
【例2】根据自相干函数的定义式（4.2.29），完成以下证明和讨论。
（1）证明场中某点在两个不同时刻的复相干度为
（2）讨论一个振荡于两个相邻频率上的激光光源，这两个相邻频率的频差约为108Hz。假设这两个频率中的每一个频带都无限窄，计算|γ11（τ）|。
【解】（1）根据定义式（4.2.14），有
再利用式（4.2.29），便得到式（4.3.40）。
（2）由于已假定每个振荡频率的频带是无限窄的，故在辐射场中它们都为δ函数分布，从而其光谱密度
（ν）可写成（参阅例3）如下形式：
式中，I1、I2分别代表两个频率的辐射强度。将上式代入式（4.3.41），并进行积分，得到
式中，γ=
，Δν=ν1-ν2。因此
因而，|γ11（τ）|不仅与Δν有关，也与γ有关。例如，当γ=1即I1=I2时，有
因而|γ11（τ）|随τ周期地变化，而当
时，复相干度等于零。如果允许相干度为
，则τ将限制在
以内。因此，对于光谱轮廓近似为高斯型和半宽度约为104Hz的单频激光器，由式（4.1.20）知，其相干长度约为30 km；而当Δν≈108Hz时，相干长度减小到大约300 cm。
【例3】对于频率为ν0的完全单色光源发出的辐射场，可以写成
试证明
（ν）=u20δ（ν-ν0），因而
（ν）将是光源的光谱分布的度量。
【解】根据定义，有
而
（ν）是Γ11（τ）的傅里叶变换，故得
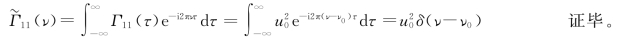
本章重点
1.光源的空间相干性和时间相干性。
2.互相干函数和复相干度。
3.准单色光的传播。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
