在实际用来传输、存储和处理信息的光学系统中，最常用的是准单色光波场，这种光波的频率成分只限于一个在中心频率ν0附近的窄带Δν范围内，且满足条件Δν≪ν0，其他频率成分都为零。此外，从相干性考虑，还应确保光路中从光源到干涉区域所涉及的最大光程差远小于光的相干长度LC，或
光束的干涉实验是揭示光场互相关联程度的最简易而又最直接的方法。因而下面的讨论仍然以图4.1.1所示的杨氏干涉装置为基础。
根据公式（4.2.27），互相干函数可以表示为
考虑到准单色光条件，只有在|ν-ν0|≤
的频率上，
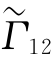（ν）才有明显不为零的值，亦即上式中对积分主要的贡献来自|ν-ν0|≤
的很窄的频带内
。此外，式（4.3.1）意味着τ≪τ0=
。其结果是确保在感兴趣的观察区域内，条纹对比度为常数。在上述条件下，式（4.3.2）积分中的复指数可近似等于1，因而式（4.3.2）可改写成
而由式（4.2.27）可知
于是有
现定义互强度J（P1，P2）或J12表示P1、P2两点在t时刻（相对时延τ=0）光振动的互相关：
则式（4.3.5）可改写成
用类似方法可得
再定义μ（P1，P2）或μ12表示复空间相干度γ12（0）：
则式（4.3.8）可以写成
(www.xing528.com)
若令
则在准单色光近似下，P点辐射场的干涉规律式（4.2.19）变为
由以上讨论可知，|μ12|与α12（0）都是与τ无关的量。如果I1（P）和I2（P）在观察区域内近似不变，则在该区域干涉图样具有几乎恒定的对比度和位相。条纹对比度为
若两束光的强度相等，即I1（P）=I2（P），则
即在两列光波强度相同的条件下，条纹对比度由其复空间相干度的模决定。因此，只要测量出干涉条纹的对比度，便可以确定复空间相干度的模|μ12|。干涉条纹的最大值出现在：
测量出干涉极大值的位置就可以确定复空间相干度的位相α12（0）。
将式（4.3.12）与式（4.2.19）相比较可以看出，准单色光场类似于频率为ν0的严格单色光场。区别在于准单色光的干涉条纹的对比度和位置分别取决于复空间相干度的模和位相。当|μ12|=0时，干涉条纹消失，两束准单色光呈非相干叠加；当|μ12|=1时，条纹最清晰，对比度最大，呈现相干情况。当0＜|μ12|＜1时，两个光波是部分相干的。图4.3.1给出3种典型情况下的强度分布。
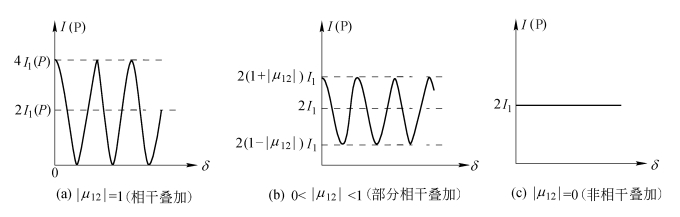
图4.3.1 具有相同强度的两准单色光波的叠加（δ=2πν0τ）
在用于描述光场相干性的物理量Γ12（τ）和γ12（τ）中，既包含时间效应也包含空间效应。只有在准单色光场情况下才有可能把空间相干性效应分离出来。在许多光学问题中，常常可以满足窄谱线和小光程差的准单色假定。这时可以用更简单的J12和μ12作为相干性的量度，将会方便得多。
表4.3.1列出了描述光场相干性的各种参数。
表4.3.1 光场的相干性参数
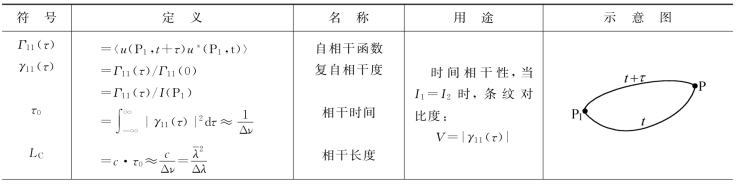
续表
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
