信息光学理论应用：测互相干函数与复相干度

前面已指出，互相干函数与复相干度是两个重要的物理量，用以表示光场中两个不同空间点的光扰动的相关程度。它们是两个可测量的物理量。测量的方法很多，基本通过实验由观测干涉条纹的清晰程度来确定。由公式（4.2.17）可以看出，为了对图4.1.1中任一给定点P，由小孔P1、P2以及给定的任何一个τ值（按r2-r1=cτ）求出Re[γ12（τ）]的值，只要测定P点的总光强I（P）以及来自每一个小孔的光强I1（P）和I2（P）即可，利用这3个测量值，再由下式计算：

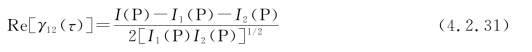
为了进一步确定Re[Γ12（τ）]，由式（4.2.14）知，还必须测量每一个小孔处的光强I1（P1）和I1（P2），即Γ11（0）和Γ22（0），再将式（4.2.31）代入，由下式：

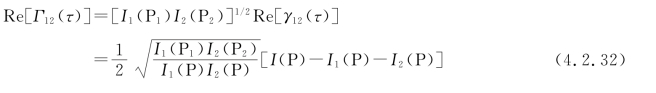(www.xing528.com)

进行计算。上述方法测量的是互相干函数和复相干度的实部，要测量它们的幅值|γ12（τ）|和位相偏离β（τ），需要利用观察平面上的干涉条纹分布。根据式（4.2.19），在干涉条纹出现极值的地方，可由其几何尺寸和用上述方法测量出的观测值计算振幅|γ12（τ）|、参数τ和β（τ）。其他位置，即参数τ不对应极值时的复相干度可由适当的插值方法计算。此外，也可通过测量干涉条纹对比度来计算复相干度。例如，由式（4.2.21）知，当两束光波在P点的强度相等时，复相干度的模就等于干涉条纹的对比度。

最后指出，互相干函数和复相干度的测量不仅仅是空间相干性的测量。在杨氏实验装置中，采用有限谱宽的扩展光源照明两个小孔，观察屏上干涉条纹的对比度从中心向两侧逐渐减小。这一物理现象包含了空间相干性效应，也包含了时间相干性效应。只有在零光程差或者τ=0附近，干涉条纹的对比度才反映同一时刻点P1和点P2光振动的互相关性质，即单纯的空间相干性效应。