信息光学理论与应用：实多色场的复值表示详解

为了研究光场的相干性，需要一个矢量函数来全面地描述辐射场。但假如只考虑小角度发射的辐射，并且不考虑辐射场的偏振效应，则用一个标量函数来描述辐射场，对于研究经典相干理论的大部分概念，还是令人满意的。

假设空间某点r在时刻t的光场可以用一个实标量函数ur（r，t）来描述。为了简化书写，下面略去空间变量r，记为ur（t）。对于线性系统，常常把ur（t）表示成与之相关联的一个复函数：

更便于运算，式中ur（t）、ui（t）分别表示u（t）的实部和虚部。u（t）称为ur（t）的解析信号（Analytic Signal）。

对ur（t）作傅里叶分解，得到

式中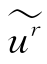，（ν）是ur（t）的傅里叶谱。由于ur（t）是实函数，故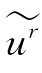（ν）应是厄米特函数：

上式表明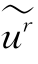（ν）的负频率分量与正频率分量载有同样的信息，亦即仅正频率分量（或负频率分量）就携带了实函数的全部信息。因此，只用正频率分量并不会丢失光场的任何信息。令

则由式（4.2.3）显然有(www.xing528.com)

即A（ν）是偶函数，φ（ν）是奇函数。将式（4.2.4）代入式（4.2.2），并取其中对应的正频率和负频率项相加，利用欧拉公式可将式（4.2.2）最后表示成

上式包含所有正频率分量的积分。若把这些频率分量都相移，则可定义函数ui（t）为

因而与ur（t）相关联的解析信号可写成

式中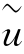，（ν）是函数u（t）的频谱，u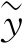（ν）与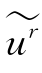（ν）的关系可以表示成

式（4.2.8）表明，去掉实函数ur（t）的所有负频率分量，并把正频率分量的幅值加倍后叠加起来，就得到了解析信号u（t）。反之，实函数ur（t）可由它的解析信号u（t）唯一确定：

式中，Re表示取实部。同样，函数ui（t）也可以由函数ur（t）唯一确定，因为从ur（t）中把每一个傅里叶分量的位相变化后，就可得到ui（t）。因此，积分式（4.2.6）和（4.2.7）称为同源的傅里叶积分，亦称为相缔合的函数（Associated Function）。