光源的时间相干性及光波频谱-信息光学理论与应用

光源的时间相干性（Temporal Coherence）是指在同一空间点处，在任意相等的时间区间Δt内测得该点的位相差都不随时间而变。光源的时间相干性取决于光源的频谱宽度Δν。我们知道，实际的光源都是以不连续的许多有限长的波列形式（称为“波串”，Wave Train）来发射光波的（如图4.1.3所示）。而任何有限长的波列必然包含着不同波长的光波，只有纯单色光才是无限长的波列。在图4.1.3中画出了辐射场随时间变化的一种情况，图中τ0代表各个波列的平均持续时间。不同波列之间没有确定的位相关系。因此，如果时间间隔Δt≪τ0，则在t与（t+Δt）时刻的两个光场具有确定的位相关系；而对于Δt≫τ0的两个光场，即使是由同一光源发出的光波，它们之间也几乎没有任何位相关系。在Δt大致等于τ0的时间间隔内，即可说这两个光场仍然是相干的。τ0称为辐射的相干时间（Coherent Time），相应地波列的长度称为相干长度LC（Coherent Length），且

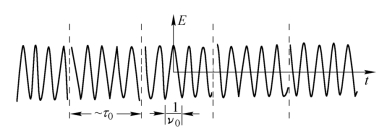
图4.1.3　辐射场随时间的变化举例

式中，c为真空中的光速。通常就用相干长度和相干时间来衡量时间相干性的好坏。

为了进一步领会辐射的时间相干性，再来看一下迈克尔逊干涉仪。如图4.1.4所示，它由两个彼此垂直的平面镜M1、M2和一个分光镜BS组成，分光镜等分两平面镜之间的夹角，并且让入射平面波一半透过、一半反射，形成两个平面波，它们经各自的传播路径后在干涉仪输出端重新会合，形成干涉条纹。仔细调整干涉仪，当两列光波传播的距离相等时，所得条纹的对比度特别好，V=1，暗条纹完全是黑的，如图4.1.4（a）所示。现在假定将反射镜M1缓慢地向后平行移动而使干涉仪的一个臂延伸一段距离，以增加光程差，则此时所得到的条纹图样将具有稍差一些的对比度，例如使V=0.5，如图4.1.4（b）所示；如果反射镜M1进一步移动，则条纹对比度将进一步降低，直到条纹消失，V=0，如图4.1.4（c）所示。

图4.1.4　用迈克尔逊干涉仪演示时间相干效应

条纹消失的原因是，当M1移动距离后，在两臂中引进了Δl的光程差，从而使M1反射来的光波较之从M2反射来的光波推迟了秒，如果≫τ0，则分别从M1、M2反射来的两列光波之间无任何位相联系，故不能形成干涉条纹。反之，如果≪τ0，则两列光波之间有确定的位相关系，故能满足相干条件且干涉条纹有较好的对比度。迈克尔逊干涉仪中这种随着光程差的增加而使条纹对比度降低的现象，也是光源时间相干性的一种度量。

实际的光源所发出的光不可能是严格单色的，总有一定的频谱宽度Δν（或Δλ）。现在先考虑准单色光情况，即满足条件：

式中，Δλ=λ2-λ1，；λ1、λ2各代表谱线宽度两端的波长。观察屏上的干涉图样实际上是光源所包含的不同波长成分的干涉条纹的叠加。现假设只考虑两个极端的波长λ1和λ2所产生的两组干涉条纹，且设每一种波长的光波贡献一半的光强度。而在条纹图样中的任一点，一种波长和另一种波长之间的位相差为

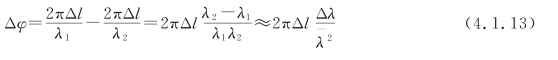
注意：代表干涉仪两个臂长之差，Δl则为两臂之间引进的光程差。

当两臂间引进的光程差达到某一极限值从而使其位相差Δφ=2π时，则波长为的第m+1级明条纹和的第m级明条纹正好重合在一起，这时在观察屏上每一点从成分的第m级到第m+1级极大之间，相继分布着由到各成分的第m级极大。换言之，观察屏上每一点都落有某一光谱成分的极大值和另一光谱成分的极小值，因而各点条纹强度趋于一个平均值，即条纹消失，如图4.1.5所示。图中实线表示的m到m+1级的条纹强度分布，A、B、C、D……是对应于光谱各成分的第m级极大值。这时对应的光程差即称为相干长度LC，其值可由式（4.1.13）得到

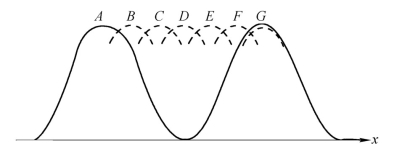
图4.1.5　准单色光从-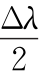到+的各个干涉极大在Δl～上的分布

如果要求条纹对比度保持大于0.9的值，则Δφ必小于，于是光程差应控制在一个规范值内，即

下面再来考察用函数f（t）所代表的有限时宽τ0的单列波所包含的频谱。f（t）随时间的变化关系由下式给出：

按照傅里叶变换理论，任一有限可积函数都可用无限个正弦分量之和来表示，因而可把这单一波列的振动f（t）看成是不同频率ν的单色振动的叠加，即

式中，F（ν）表示f（t）的单色分量的振幅分布。按照傅里叶变换的对应关系，f（t）的频谱为

将式（4.1.16）代入上式，算得

各频谱成分的归一化功率谱分布为

上述各函数关系图形如图4.1.6所示。从图4.1.6（b）看出，当ν=ν0时频谱值为最大，而在ν=ν0±时降为零。大部分能量集中在ν0两侧的两个第一级极小之间的区域（即区域）内。通常取Δν=ν-ν0为半谱线强度的宽度，遂在内的频率成分具有较大的干涉强度。因此，可视频谱分布的宽度Δν为(www.xing528.com)

图4.1.6　有限波列f（t）的频谱与功率谱

从而

由此可见，辐射为有限长波列的光波实际是由中心位于ν=ν0、宽度为Δν的各种频率的正弦波叠加而成的。上式称为时间相干性的反比公式，它表示了谱线越窄，相干时间越长，时间相干性越好。将式（4.1.19）代入式（4.1.11），并由ν=得

这与式（4.1.14）的结果一致。

必须指出，由于实际光源都是具有有限频带宽度的扩展光源，故其辐射光场的相干性应同时包含时间相干性和空间相干性的双重影响。只是对于光谱线很窄的扩展光源，应主要考虑空间相干性；对于有限频宽尺寸很小的光源，则主要考虑时间相干性。

激光器是同时具有优良的空间相干性和时间相干性的光源，一般对全息照相和全息干涉计量而言，总希望所用的激光光源具有更长的相干长度，因为它决定了光路布置中物光和参考光束之间所允许的最大光程差。在激光器问世以前，大多数干涉仪采用滤光水银灯作光源，其相干长度约在0.03～0.2 mm量级，而现在普通1 m长的连续波He-Ne激光器却具有20 cm量级的相干长度，而且以损耗一些功率为代价，可以将它改进成单纵模输出，因而可将其相干长度增加到数米甚至更长。国内现已有长相干He-Ne激光器产品问世，其相干长度可达十余米，而输出功率在50 mW左右。

【例1】试分析由非单色光源照明的杨氏双缝干涉实验。

【解】设光源的频谱范围是（或），并设各频率成分具有同等的强度，如图4.1.7所示。现参照图4.1.1及公式（4.1.1）、（4.1.3），并令xS=0，则得到单色光的干涉条纹强度分布为

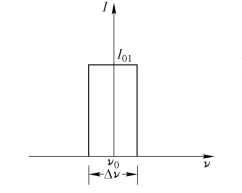
图4.1.7　光谱分布为平顶型

式中，I01为单孔（或缝）在观察点P（x）处的光强度。而中心频率为ν0、频带宽度为dν的光波的强度为I01dν，在P（x）点处产生的干涉条纹强度为

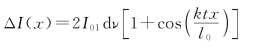
则在P（x）点处由各频谱成分产生的总光强分布为其积分：

完成积分，将代入并应用三角公式，最后得

其中

即条纹对比度。

在观察屏中心x=0处，V（x）=1，条纹最清晰；而当=n（n为整数）时，V（x）=0，干涉条纹消失。条纹第一次消失时为n=1，此时有

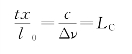
干涉条纹的位置由决定。其条纹强度分布如图4.1.8所示。

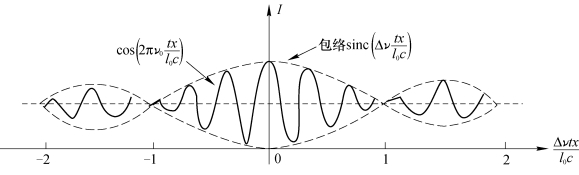
图4.1.8　光源单色性对干涉条纹清晰度的影响

附带指出，在上面的分析中，将光谱分布假定为平顶型过于简单。事实上，光谱分布有多种类型（典型的还有高斯型谱线、洛仑兹型谱线等），进一步的分析可参考本章参考文献[1]。