光源的空间相干性与光源线度-信息光学理论与应用

研究光场的相干性就是要研究光场中任意两点的光扰动相叠加时的表现，并根据这种表现来确定光场的相干性。为了讨论光场中任意两点光扰动的叠加，就要把这两点的光扰动引出来并使之相遇。最简单的办法就是利用杨氏双孔（或双缝）干涉装置，观察由双孔干涉产生的条纹图样。

图4.1.1表示一简单的杨氏双孔实验装置。首先考虑光源S是单色点光源的情况，该点光源位于图中xS处，略高于对称轴一个微小距离xS，并设其在P1、P2处形成的光场基本相同，它们经小孔P1、P2衍射后在观察屏上形成干涉条纹。干涉场的强度分布由下式决定：

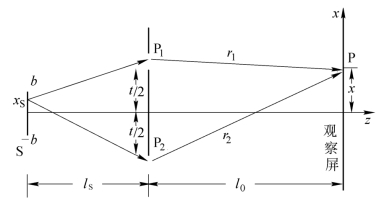
图4.1.1　单色点光源的杨氏双孔干涉

式中，δ=k（r2-r1）=kΔr，r1、r2各代表由点源xS经小孔P1、P2到达观察点P的光程，并设I1=I2=I01。由图4.1.1求得

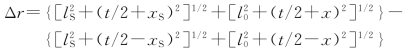
将上式整理后得

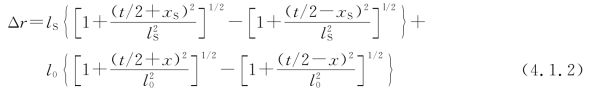
由于xS、x和t比l0及lS小得多，故可用关系式（1±ε2）1/2≈1±，得到式（4.1.2）的近似式：故强度分布公式（4.1.1）最后可写成

式中，I0为观察屏上的最大光强。由式（4.1.4）知，在x取定值处，观察屏上的光强度相同；x取不同值处，光强度则不同，从而出现直线条纹。其条纹间隔Δx由下式决定：

由此求得

因此，观察屏上为一系列间隔为的平行条纹。但在实际情况下，观察屏上能否看到干涉条纹，在多大范围内能看到干涉条纹，这与光源本身的性质和光路布置有关。了解这些情况就可以有效地使用光源和合理地安排光路，以满足对光源相干性的要求。

以上讨论尚未涉及光源尺寸的影响。现在假设图4.1.1中的S不是点光源，而是线光源，则由于光源S有一定线度，其中每一个点都独立发光。虽然所有点发出的光波的波长都是相同的，但在此光源上点与点之间的位相变化都是随机的。因而来自光源上一个点的光与来自其他点的光都是非相干的，这样每一个点发出的光通过小孔P1、P2后都在观察屏上单独形成一组杨氏干涉条纹，每组条纹也是等距平行的，但沿垂直于条纹方向相互错开了一段距离，从而使各自的明暗条纹交错重叠，降低了整体条纹图样的对比度。

由光源上一点xS处发出的光在观察屏上任一点x处的强度由公式（4.1.4）给出。而整个光源在观察屏上x处的总强度则可由该式在光源宽度2b上积分得到，即

应用三角公式cos2（x）=[1+cos（2x）]/2，代入上式积分，再利用三角公式：

经过变换，最后得到(www.xing528.com)

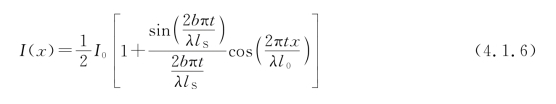
这些条纹的对比度为

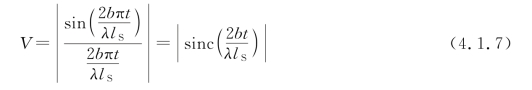
此函数图形如图4.1.2所示。显然，只有当光源尺寸趋于零（即b≈0）时，条纹对比度才最好（V=1），随着光源尺寸的增加，条纹对比度降低，相干性变差。当光源尺寸满足：

即

时，条纹消失，故得光源的极限尺寸（或称光源的临界宽度）为

式中，α=是图4.1.1中两小孔P1和P2点对光源中心的张角，称为干涉孔径角（Interference Aperture Angle）。所以，只有光源尺寸小于2bC时，点P1、P2间的光振动才存在相关，观察屏上才会出现干涉条纹。

从图4.1.2的曲线还可以看出，当光源宽度不超过其临界宽度的时，条纹对比度V＞0.9，干涉条纹仍清晰可见。因此，欲使干涉条纹有较好的清晰度，光源的尺寸应进一步减小到

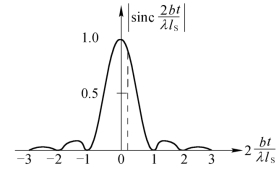
图4.1.2　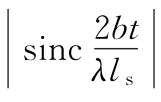函数图形

由上式所决定的光源宽度称为光源的许可宽度，可用来计算干涉装置中光源线度的允许值。

从另一角度来说，对于选定的光源尺寸2b，两个小孔的距离t越小，干涉条纹就越清晰，而随着t增大，干涉条纹对比度下降，直至条纹最后消失。两小孔间最大允许间隔应为

式中，β=是扩展光源对小孔连线中点的张角。tC也称为横向相干宽度（Breadth of Transverse Coherence）。当β确定以后，距离超过tC的空间两点（孔），它们的光振动不存在相关。同样，欲使干涉条纹有较好的清晰度，两小孔的间距也应进一步减小到

公式（4.1.9）表示光源极限尺寸与干涉孔径角成反比；公式（4.1.10）表示横向相干宽度与光源张角成反比。这两个公式是等效的，统称为空间相干性的反比公式。

通过上述讨论，说明所谓空间相干性（Spatial Coherence），是指在波面上固定两点的位相差与时间无关，它描述在同一时刻波面上两点之间光场的相干性。激光器的空间相干性与谐振腔的横模结构有关。大多数连续波激光器都容易实现单横模（TEM00模）输出，在此种工作模式下，波面上的各点实际上是同位相的，因此它们具有特别好的空间相干性。