信息光学：相干与非相干成像系统的对比

本节将对相干成像和非相干成像两种系统做一些比较，并作为本章的小结。通过这种比较，虽然并不能简单地得出哪一种照明方式更优越，但有助于读者更加深入地理解这两种系统之间的联系及其某些差异，从而可根据一些具体情况判断选择哪一种照明方式会更加适合。

1.截止频率

由前两节的讨论看到，非相干衍射受限系统OTF的截止频率扩展到相干系统CTF的截止频率的两倍处。因此似乎可以得出结论：对于同一个光学成像系统，使用非相干照明一定会比采用相干照明得到更好的像。可是从下面的讨论将看到，这个结论一般是不正确的。其主要原因在于，相干系统截止频率是确定像的复振幅的最高频率分量，而非相干系统截止频率是对像的强度的最高频率分量而言的。虽然在这两种情形中，最后的可观察量都是像的强度分布，但由于两种截止频率所描述的物理量不同，所以不能直接对它们进行比较，而简单地得出结论。

2.两个点物间的分辨

分辨率是评价光学系统成像质量的一个重要指标。对于衍射受限的圆形光瞳，在非相干照明方式下，根据瑞利分辨判据，若两个强度相等的非相干点源，一个点源产生的艾里斑中心恰好落在另一个点源所产生的艾里斑的第一个极小上，则称它们是非相干衍射受限系统“刚刚能够分辨”的两个点源。由2.5节中圆孔的夫琅和费衍射花样公式（2.5.16）知，像斑的归一化强度可表示为

式中，x=。又由表2.5.1可知，第一个暗环的角半径为x=1.22，所以，如果把两个点源像的中心沿x轴方向分别放在x=±0.61处，则它们正好满足瑞利分辨判据的条件，且其光强分布可表示为

图3.5.1（a）画出了此强度分布的剖面图，此时，两个点源的艾里斑图样在其中心处约下降26.5%，对应的鞍峰比为73.5%（如果是两条狭缝产生的衍射，则对应的鞍峰比为81.1%）。

对于相干照明方式，两个点源产生的艾里斑则必须先按复振幅叠加，再求其合强度。此强度记为

式中，φ是两物点之间的位相差。显然，I（x）的值与φ有关。在图3.5.1（b）中画出了φ=0°，90°和180°时的光强分布。根据图3.5.1中的曲线，可以对系统在相干照明和非相干照明条件下的分辨能力进行比较后，得出如下结论：

图3.5.1　相距为瑞利极限的两个点源像的强度分布

（1）φ=0°，即两点源同位相时，I（x）不出现中心凹陷，因而两物点完全不能分辨，其分辨能力不如非相干照明的情形好。

（2）φ=90°时，相干照明的强度分布I（x）与非相干照明所得结果完全相同，从而在两种照明方式下，系统的分辨能力一样。

（3）φ=180°，即两点源位相相反时，相干照明的强度分布I（x）的中心凹陷取极小值，远远低于26.5%，故这两点比非相干照明方式下分辨得更清楚。

由此可见，到底哪种照明方式对提高两点源间的分辨率更为有利，我们不可能得出一个普遍适用的结论。故瑞利判据仅适用于非相干成像系统，而对于相干成像系统，能否分辨两个点源，则要考虑它们的位相关系。

3.像强度的频谱

在相干照明和非相干照明下，像强度可分别由式（3.2.19）、式（3.2.22）表示为

对以上两式进行傅里叶变换，并利用卷积定理和相关定理，得到相干照明和非相干照明方式下像强度的频谱分别为式（3.5.3）、式（3.5.4），即

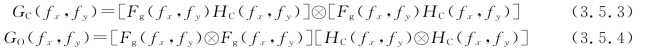(www.xing528.com)

式中，GC（fx，fy）和GO（fx，fy）分别是相干和非相干系统中像强度的频谱。就频谱内容而言，从上列两式不能简单地得出结论来说明一种照明方式比另一种照明方式更好。但上列两式表明，两种照明方式下的频谱内容可以很不相同。因为成像结果不仅与照明方式有关，也与系统的结构和物的空间结构有关。这一点可从下面的两个例题中得到进一步的理解。

4.对锐边的响应迥然不同

由相干成像系统的传递函数公式（3.3.4）：

可知，该函数具有陡峭的不连续性，且在截止频率确定的通频带内不衰减，因而具有较小的误差。

而非相干成像系统的传递函数为式（3.4.14）：

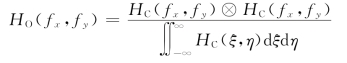
它在截止频率所确定的通频带内，不像HC（fx，fy）那样恒等于1，而是随空间频率的增大逐渐减小，其结果是降低了像的对比度。

【例1】有一单透镜成像系统，其圆形边框的直径为7.2 cm，焦距为10 cm，且物和像等大。设物的透过率函数为

式中，b=0.5×10-3cm。今用λ=600 nm的单色光垂直照明该物，试解析说明在相干光和非相干光照明的情况下，像面上能否出现强度起伏？

【解】按题设条件，物周期，其频率线/毫米；而d0=di=2f=200 mm，故fC==300线/毫米，f0==600线/毫米。显然，在相干照明条件下，fC＜f1，系统的截止频率小于物的基频，此时，系统只允许零频分量通过，其他频谱分量均被挡住，所以物不能成像，像面呈均匀分布。在非相干照明下，f1＜f0，系统的截止频率大于物的基频，故零频和基频均能通过系统参与成像，在像面上将有图像存在。基于这种分析，非相干成像方式要比相干成像方式好。但在别的物结构下，情况将发生变化（见例2）。

【例2】在例1中，如果物的透过率函数换为

结论又如何？

【解】这时，物周期T1=b，其频率f1==200线/毫米。根据例1的数据，显然f1＜fC＜f0，即在相干照明下，这个呈正弦分布的物函数复振幅能够不受衰减地通过此系统成像。而对于非相干照明方式，物函数的基频也小于其截止频率，故此物函数也能通过该系统成像，但其幅度会随空间频率的增加产生逐渐增大的衰减，即对比度降低。由此可见，在这种物结构下，相干照明方式要比非相干照明方式好。

此外，相干照明具有严重的散斑效应（详见第9章），且光学缺陷易在相干照明下观察到，并容易产生一些木纹状的附加干涉花纹，对成像的清晰度带来干扰。

本章重点

1.薄透镜的位相调制作用、傅里叶变换性质和成像特性。

2.HC（fx，fy）和HO（fx，fy）的计算。

3.光学系统的截止频率。

4.像强度分布的计算。