信息光学理论应用：像差对OTF的影响

对于有像差的光学系统，不论造成像差的原因是什么，总可以归结为波面对于理想球面波的偏离。因此，仿效前节对公式（3.3.10）的讨论，可用广义光瞳函数替代光瞳函数，写成

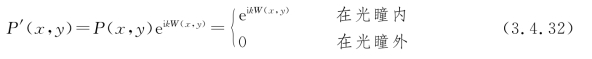
将上式代入式（3.4.23b）中，便得

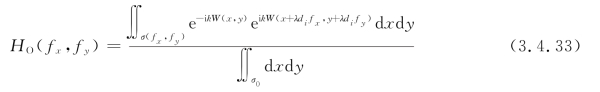
上式把波面的偏差（即像差）与OTF直接联系了起来。

利用Schwarz不等式可以证明，像差的存在不会增大MTF的值。为此，在式（3.4.19）中，令

X=exp[-ikW(ξ,η)]

Y=exp[ikW(ξ+λdifx,η+λdify)]

将式（3.4.33）两端取模的平方，再应用Schwarz不等式（3.4.19），同时注意到|X|2=|Y|2=1，便得到

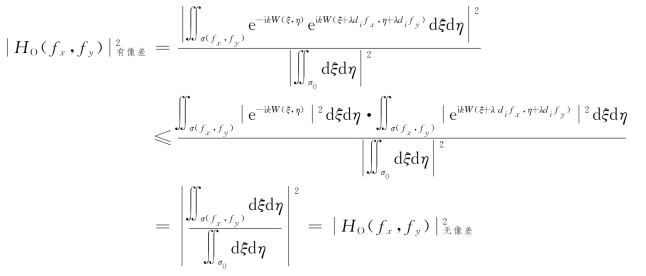
将两端开平方后有

即

由此可见，像差的存在会使光学系统的调制传递函数下降，使像面光强度分布的各个空间频率分量的对比度降低。但可以证明，对于有像差系统和无像差系统，只要是同样大小和形状的出射光瞳，其截止空间频率都是相同的。

【例1】计算存在聚焦误差时的OTF。为简单起见，设系统的出瞳是正方形，边长为l。像差仅仅是由像面位置没有与理想像面重合而引起的。（严格地说，离焦实际上不是像差，而是调焦不准确。）

【解】根据公式（3.4.33），为求此时系统的光学传递函数HO（fx，fy），应先确定波像差eikW（x，y）。为此可参看图3.4.4。实际像面位于理想像面右方Δ处；实际波面W1对应的像点为P′i。P′i像点所要求的理想球面波面为W0，因而在过P′i点的面上产生离焦像。像差可以看成是广义光瞳函数eikW（x，y）的作用。而eikW（x，y）应等于两个球面波的位相偏差：

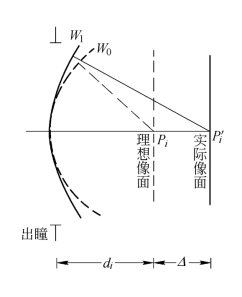
图3.4.4　光学系统的聚焦误差

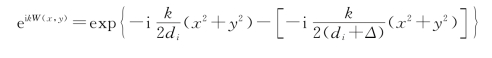
式中，ε表征离焦的程度，即(www.xing528.com)

对于边长为l的正方形光瞳，沿x轴和y轴方向，孔径边缘上的最大光程差WM为

广义光瞳函数可写为

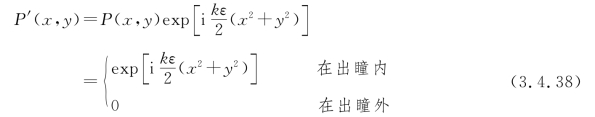
系统的相干截止频率（或l=2λdifC），而W（x，y）=（x2+y2）=（x2+y2）=。把它们代入式（3.4.23b）中，并认为两个错开（λdifx，λdify）的光瞳是各自朝相反方向移动和后形成的，遂有

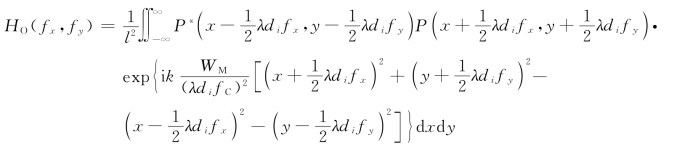
上式积分号中指数因子经整理可化为

而两个错开光瞳的重叠面积为

σ(fx,fy)=(l-λdi|fx|)(l-λdi|fy|)

所以

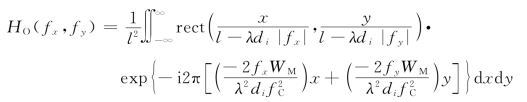
遂由傅里叶变换相似性定理，得到

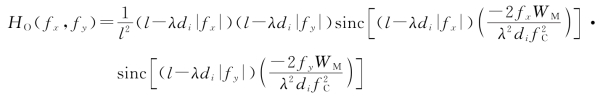
将代入上式，并考虑到sinc函数是偶函数，经整理化简后得

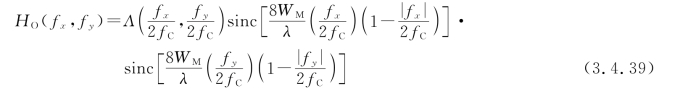
上式就是因调焦不准确对OTF产生影响的表达式。在图3.4.5（a）中画出了，和λ时的HO（fx，0）曲线。由图中看到，当WM=0时，得到衍射受限成像系统的OTF曲线。当时，OTF曲线接近上述理想情况，这说明离焦的光程偏差不超过λ4时，其对成像质量影响不大，从而可以把作为离焦的容限。当时，OTF在某些区域出现负值，对应频率成分产生π的相移，这表示该区域的对比度发生了翻转，即强度峰值变为强度零点，反之亦然〔见图3.4.5（b）〕。这种现象通常称为伪分辨（False Resolution）。

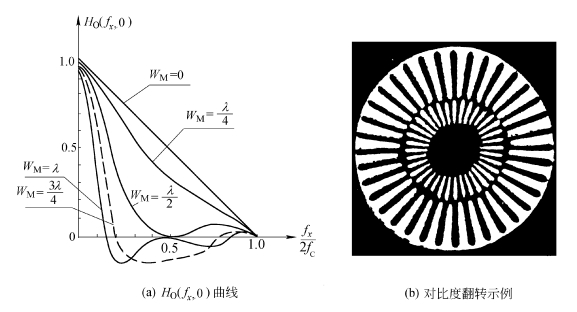
图3.4.5　正方形光瞳系统有离焦像差时的OTF