信息光学理论与应用：快速计算衍射受限系统OTF

由于衍射受限成像系统的相干传递函数HC（fx，fy）与光瞳函数P（x，y）之间有下列关系：

HC(fx,fy)=P(λdifx,λdify)

而且光瞳函数只取两个实数值，即0和1，故有

HC(fx,fy)=H*C(fx,fy)

|HC(fx,fy)|2=HC(fx,fy)

将上列各式代入式（3.4.14）中，有

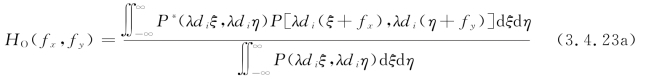
令x=λdiξ，y=λdiη，则上式可改写成

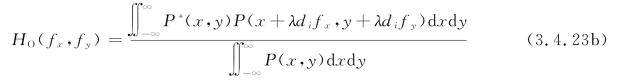
显然，光学传递函数也是光瞳函数的归一化自相关。上式还给OTF一个重要的几何解释，由此便可导出OTF的计算公式。由于P（x，y）只取0和1两个实数值，故式（3.4.23b）中的分母代表光瞳的总面积σ0；而分子中的P（x+λdifx，y+λdify）只是将光瞳函数P（x，y）分别沿x轴方向和y轴方向移动-λdifx和-λdify，光瞳并未改变，并且只有在它们都不为0的区域内，被积函数才不为0且取值为1，故分子表示两个错开的光瞳相互重叠区的面积σ（fx，fy），如图3.4.1中的阴影部分所示。因此，可以对OTF做出这样的几何解释：

上述几何解释又再次表明，衍射受限非相干成像系统的OTF恒为非负的实数，因此它只改变各频谱分量的对比度，而不产生相移。

根据公式（3.4.24），可以将计算衍射受限非相干成像系统的OTF的步骤归纳如下：

（1）确定系统出瞳的形状和大小，计算出瞳总面积σ0。

（2）计算出瞳面至像平面之间的距离di。

（3）任意给定一组（fx，fy）值，算出（λdifx，λdify）值；将出瞳平移，使其中心落在（-λdifx，-λdify）处，计算移动前后两出瞳的重叠面积。

（4）相继再给定一组（fx，fy）值，算出重叠面积。依此类推，就可算出σ（fx，fy）。

（5）按照公式（3.4.24）计算σ（fx，fy）/σ0，最终得到HO（fx，fy）。

当出瞳的几何形状比较简单、规则时，可以求出HO（fx，fy）的完整表达式。对于形状复杂的出瞳，可以用计算机或面积仪求出HO（fx，fy）在一系列分立频率上的值。

根据上述计算步骤并结合图3.4.1，还可以确定衍射受限非相干成像系统的截止频率（f0x，f0y）。下面结合两个计算实例予以说明。为了与相干照明的情况相比较，仍分析方孔和圆孔光瞳。

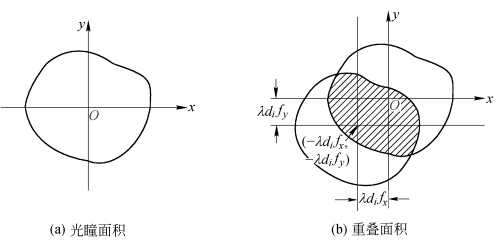
图3.4.1　衍射受限系统的OTF计算

【例1】设衍射受限非相干成像系统的出瞳是边长为l的正方形，求其OTF。

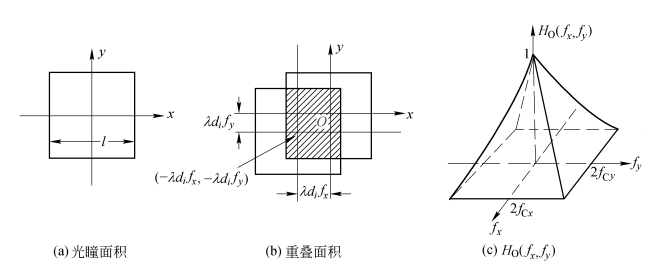
【解】如图3.4.2所示，出瞳总面积σ0=l2。重叠面积由图3.4.2（b）中的阴影部分可以求得

(www.xing528.com)

图3.4.2　出瞳为正方形的系统的OTF计算

所以

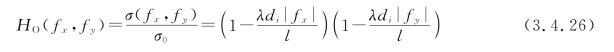
显然，只有当λdi|fx|＜l且λdi|fy|＜l时，HO（fx，fy）才有不为零的值，由此求得该系统的截止频率为

将相干系统的截止频率关系式（3.3.15）代入式（3.4.26）中，并由三角形函数定义式（1.1.10），得

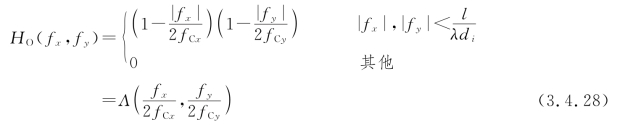
其图像如图3.4.2（c）所示。

【例2】衍射受限非相干成像系统的出瞳是直径为D（=2r）的圆，求该系统的OTF。

【解】在此情况下，OTF显然是圆对称的，故只需沿fx轴正向计算HO（fx，fy）就足够了。如图3.4.3（b）所示，重叠面积（图中阴影部分）被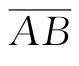分成面积相等的两个弓形。由几何学公式可知

于是容易求得光瞳重叠面积为

σ(fx,0)=r2(2θ-2sinθcosθ)

而出瞳总面积为σ0=πr2。最后可求得

或写成

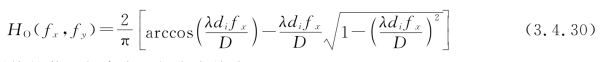
由圆对称性可得系统的截止频率在一切方向均为

该传递函数的图像如图3.4.3（c）所示。

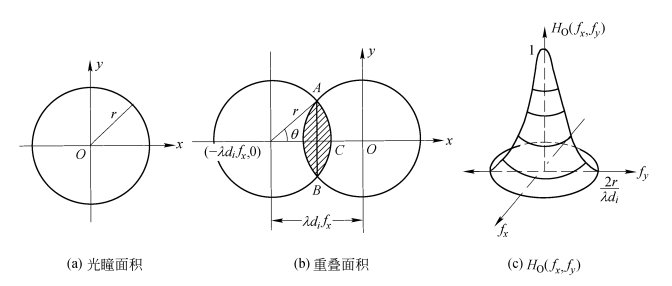
图3.4.3　出瞳为圆形的系统的OTF计算

将式（3.4.27）、（3.4.31）与式（3.3.15）、（3.3.18）比较可以看出：非相干成像系统的截止频率是相干成像系统的两倍。但从它们各自的图像上看到，在截止频率以内，OTF的值不像CTF那样恒为1，而是随空间频率的增大逐渐减小。