信息光学理论与应用：光学传递函数的一般性质及意义

OTF描述非相干照明下系统的成像性质，它反映系统本身的属性，而与输入物函数的具体形式无关。以下是OTF的几个重要性质。

上式可由定义式（3.4.11）令其分子中fx=fy=0而直接得证。它表示光学系统对零频信息总是百分之百地传递。

这是因为h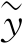I（x，y）=|h（x，y）|2是实函数，故其傅里叶变换谱必然具有厄米特函数特性。

即MTF是偶函数，PTF是奇函数。上式可由性质（2）直接证明。

上式的物理意义是：任意空间频率的MTF必低于零频下的值1。故非相干光学成像系统也可以看作是一个低通空间频率滤波器。

为了证明式（3.4.18），要用到Schwarz不等式：

其中，X（ξ，η），Y（ξ，η）是ξ，η的任意两个复函数，等号只有当Y=KX*时才成立，K是复常数。

由于X，Y是任意的复值函数，故可令

将此关系式代入式（3.4.19），得

上式两端先开方，再除以（归一化）即得证。|H（fx，fy）|永远不大于1。

顺便指出，虽然OTF在零频下其值恒为1，但这并不意味着像的本底绝对强度水平与物的本底的绝对强度水平相同。OTF定义中所用的归一化已经消除了关于绝对强度水平的一切信息。

下面再讨论OTF的一般意义。(www.xing528.com)

在式（3.4.1）中，令

并取fx=fy=0，则由该式得

又由式（3.4.12）知

在归一化条件下，必有

从而有

式中，Vi（fx，fy）和Vg（fx，fy）分别表示系统的输出像和输入物（理想像）各频率分量的对比度。由上式显然有

即MTF描述系统对各种频率分量对比度的传递能力，而PTF则描述系统对各频率分量施加的相移，它体现了实际的像强度分布Ii（xi，yi）的位置相对于其对应的物强度分布IO（x0，y0）〔或理想像强度分布Ig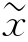（0，y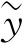0）〕移动了多少。

对于衍射受限非相干成像系统，其HO（fx，fy）为正实数，因此，它只改变各频率分量的对比度，而不产生相移，即只需要计算MTF。另外，由OTF的性质（1）和（4），有

上式表明，对于光学成像系统而言，其像的对比度不可能大于物的对比度。此外，由式（3.4.21）可以看出，当HO（fx，fy）=0时，必然有T（fx，fy）=0。这就意味着，只要空间频率（fx，fy）大于系统的截止频率，不论物的对比度有多大，像的对比度总是为零。这时，任何光能量接收器（包括肉眼和探测仪器）再也不能感知到像的结构。因此，任何光能量接收器都有一个对比度阈值VC，仅当像的对比度Vi＞VC时，像的结构才能被分辨。与对比度阈值VC相对应的空间频率，就是成像系统的分辨极限。

式（3.4.20）和式（3.4.21）还表明，可以通过分别测量调制传递函数和位相传递函数来确定光学传递函数。为此，先制作一定空间频率的余弦模板置于物方，而在像方用狭缝扫描，实行相关运算，以测定像方强度分布的对比度和平移量，从而决定一定空间频率下的|HO（fx，fy）|值和φ（fx，fy）值（参考习题1.9）。此法的关键是制作具有良好性能的各种空间频率的余弦模板，并对不同空间频率的余弦模板重复上述测量过程，以获得完整的MTF函数曲线。目前已有专门的仪器测量光学成像系统的MTF。