信息光学理论应用：相干传递函数与系统物理性质联系

由式（3.3.2）和（3.2.6），并应用迭次变换定理，当0=0，y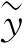0=0时，有

若将光瞳面上的坐标取反演形式，则上式中P所含的负号可略去。实际上，光瞳函数大多是关于光轴呈中心对称的，故舍去其中的负号不会产生实质性的影响。遂可将HC（fx，fy）直接表示成

上式表明相干传递函数在数值上等于系统的光瞳函数。这样就把相干传递函数与表示系统物理属性的光瞳函数联系了起来。

根据上节对光瞳函数的定义，可以写成

式中，频域坐标（fx，fy）与其空域坐标（x，y）之间的关系为

由于出瞳的孔径沿x轴和y轴方向的线度是有限的，因此沿x轴和y轴方向的空间频率的取值也是有限的，其极大值定义为系统的截止频率（Cut-off Frequency），记为fCx，fCy，则有(www.xing528.com)

式中，xmax，ymax分别是出瞳沿x轴和y轴方向的线度。由于出瞳的取值不是1就是0，故由式（3.3.4），对相干传递函数也有

其取值也是1或0。将上式代入式（3.3.1），得到光学系统输出像的频谱为

对于物分布中的某一空间频率分量（fx，fy），系统能否将它传递到像面上，取决于式（3.3.6）所确定的空域坐标值（x，y）是否在光瞳孔径之内。若在光瞳内，则此频率成分的平面波分量将毫无衰减（包括振幅和位相）地通过系统到达像面；若在光瞳外，则系统将完全不让这种频率成分的平面波分量通过，在像平面上完全没有这种频率成分，即系统对这种频率不予传递，是截止的，如图3.3.1所示。这就意味着，对衍射受限相干成像系统，存在一个有限通频带，在此通频带内，系统允许每一频率分量无畸变地通过；在通频带外，频率响应突然变为零，即通带以外的所有频率分量统统都被衰减掉。因此，衍射受限相干成像系统对输入的各种频率成分的作用，相当于一个低通滤波器。由此可见，截止频率（fCx，fCy）是检验光学成像系统质量优劣的重要参数之一。

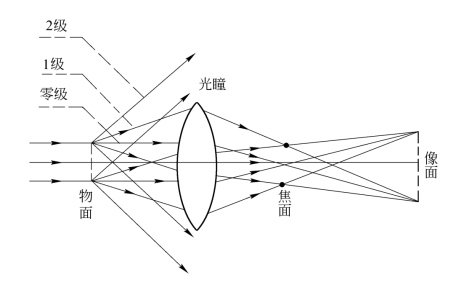
图3.3.1　光瞳对高级衍射分量的限制