衍射受限系统的点扩展函数信息光学理论与应用

前面曾提到，当物面上任意一面元产生的光振动为单位脉冲（δ函数）时，对应的像函数称为脉冲响应，亦称点扩展函数。点物的脉冲函数用δ（x-x0，y-y0）表示，相应的脉冲响应表示成

h(x0,y0;xi,yi)=S{δ(x-x0,y-y0)}

对于任意的物函数f（x0，y0），可以把它看成是由物平面上许多面元组成，每个面元具有相应的脉冲响应，由于成像系统是线性系统，当用平面单色光照明时，其像平面上光场的复振幅分布g（xi，yi）可以用叠加积分表示成

因此，只要能够确定成像系统的脉冲响应函数h（x0，y0；xi，yi），就能完备地描写该成像系统的性质。

现在将单透镜光学系统推广到复合成像系统。根据上节分析光波通过物和透镜后所得到的光场分布的一般表达式（3.1.10），用点脉冲δ（ξ-x0，η-y0）替代其中的物函数f（ξ，η），用（x，y）和（xi，yi）分别替换坐标（ξ′，η′）和（x，y）；将P（x，y）视为出射光瞳函数（简称光瞳函数），在光瞳内其值为1，在光瞳外其值为0；di代表出瞳至像平面的距离，则h就是点物经光学系统后所成的像，表示为

将上式各指数因子中的平方项展开，经合并、整理，并应用物像公式，最后得

式中，M=-是近轴条件下系统的横向放大率，根据像的倒、正，它可以取负值或正值。上式积分号外面的两个位相因子和仅表示在物平面和像平面上的位相弯曲，舍弃它们对求解像强度分布没有任何影响，于是可将脉冲响应函数写成

上式表明：单色光照明时，衍射受限系统的脉冲响应就是系统光瞳函数的傅里叶变换，其中心在几何光学理想像点xi=Mx0，yi=My0。

现对物平面坐标（x0，y0）和光瞳面坐标（x，y）作坐标变换，令

则式（3.2.4）可以写成(www.xing528.com)

上式表明成像系统是线性空间不变系统。

如果光瞳相对于λdi足够大，则在，坐标的无限大区域内，都有。这时，式（3.2.6）变为

或

因此，当不考虑光瞳的有限大小时，点脉冲通过成像系统后，其响应函数仍是点脉冲，其位置在xi=Mx0，yi=My0。这便是几何光学中理想成像时点物-点像的对应情况。

将式（3.2.7）代入式（3.2.1），在几何光学近似条件下，可得像函数为

显然，若不考虑出瞳的有限大小，则系统对物成理想像fg（xi，yi），该像与原物准确相似。

若考虑到出瞳的有限大小，则由叠加积分式（3.2.1）和式（3.2.6）得像函数为

式中，。由上式可见，像面上光场的复振幅分布等于几何光学理想像fg（xi，yi）与系统脉冲响应函数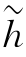（xi，yi）的卷积。这就再次表明衍射受限的成像系统可以看成是光场复振幅的线性空间不变系统。换言之，当考虑了衍射效应后，像就不再是物体的准确复现了，而是物体的平滑变形。这种平滑作用能使物体中细微结构的空间频率信息受到强烈的衰减甚至损失，从而使所生成的像产生相应的失真。