单个凸透镜能够成像,是人们从基础光学中早已熟知的事实。但大多数光学成像系统都不只限于单个透镜,它可以是由若干个透镜(正透镜或负透镜)和其他光学元件(例如棱镜、光阑等)组合成的复合系统。因此,在考察光学系统对成像的影响时,必须在若干个可能对光束起限制作用的通光孔径中,找到对光束起实际限制作用的那个孔径,该孔径可能是某一透镜的边框,也可能是光路中某一个特定光阑,我们把它称为孔径光阑(Aperture Stop)或有效光阑(Effective Stop)。由基础光学知道,孔径光阑通过它前面的光学系统所成的像,称为系统的入射光瞳,简称入瞳(Entrance Pupil,记为En.P.),它决定着进入系统的光束的大小。孔径光阑通过它后面的光学系统所成的像,称为出射光瞳,简称出瞳(Exit Pupil,记为Ex.P.),它决定着从系统出射的光束的大小,并且,入射光瞳、孔径光阑和出射光瞳三者相互共轭。
根据基础光学的讨论,一个成像系统的外部性质可以由入射光瞳或出射光瞳来描述。因此,不管成像系统的详细结构如何,都可以将它归结为下列普遍模型。光波由物平面变换到像平面,可以分为3个过程,即光由物平面到入瞳面,再由入瞳面到出瞳面,最后由出瞳面到像平面,如图3.2.1所示。当光波通过成像系统时,波面要受到入瞳的限制,从而产生衍射效应。又因入瞳与出瞳彼此共轭,故物空间入瞳对入射波的限制,变换到像空间就成为出瞳对出射波的限制。这两种限制是等价的,是同一种限制在两个空间的反映。这一结论称为光束限制的共轭原理。在考虑光波通过光学系统的衍射效应时,只需考虑其中的任何一种限制(例如,在本书中,通常是考虑出瞳对光波的衍射作用)。至于光波从入瞳到出瞳的传播,由于在此过程中波面已不再受到别的限制,故此段传播可以用几何光学很好地描述。有了光瞳的概念,在研究光学成像系统的性质时,可以不去涉及系统的详细结构,而把整个系统的成像看成是一个“黑箱”的作用,只需知道黑箱边端(即入瞳和出瞳平面)的物理性质,就可以知道像平面上合乎实际的像场分布。
为此,需要首先知道这个“黑箱”对点光源发出的球面波的变换作用。对于实际光学系统,这一边端性质千差万别,但总的来说可以分成两类,即衍射受限系统和有像差系统。在图3.2.1中,设P0(x0,y0)为物平面上任一点源,如果从该点发出的发散球面波通过成像系统后因受该系统的限制,转换成了新的理想球面波,并且在像平面上会聚成一个理想像点,则称该成像系统是衍射受限的(Diffraction-Limited)。因此,衍射受限系统的作用,就是将投射到入瞳上的发散球面波变换成出瞳上的会聚球面波。至于有像差的系统,其边端条件是:点光源发出的发散球面波投射到入瞳上,在出瞳处的透射波场将明显偏离理想球面波,偏离程度由波像差决定。后续的章节将对此进行讨论。(https://www.xing528.com)
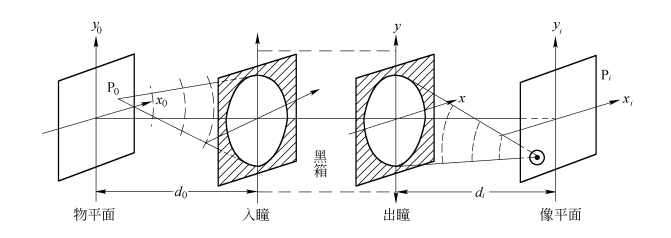
图3.2.1 成像系统的普遍模型
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




