信息光学理论与应用：傅里叶成像技术

当用单色平面光波照明一个具有周期性透过率函数的透明物体（例如透射光栅）时，将会在该物体后面某些特定距离上重现此周期结构物体的像。这种不用透镜而仅靠光的衍射就可对周期性物体成像的方法，称为傅里叶成像（Fourier Imaging），又称自成像（Self-Imaging）。这一有趣的光学现象是由泰保于1836年发现的，故又称泰保效应（Talbot Effect），并已在光学和电子显微镜等方面获得实际应用。

为了简洁起见，下面只讨论一维周期性物体。设其透过率函数为

式中，d为周期。当采用单位振幅的单色平面波垂直照明时，紧靠此物体后的光场分布即为t（x1），它可看作频率取离散值的无穷多平面波分量的线性叠加，Cn表示各平面波分量的相对振幅和位相分布。

我们的任务是研究与该物体相距z的观察平面上的光场分布。这显然是一个菲涅耳衍射问题。按照菲涅耳衍射公式（2.4.9），观察平面上的光场可表达成

上式是卷积运算形式，将它转换成频域分析会更方便些。为此，对上式作傅里叶变换并运用卷积定理，得

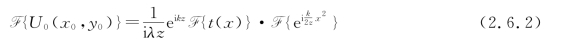
其中

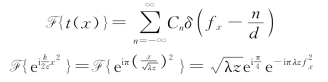
上式用到了编码脉冲信号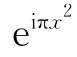的傅里叶变换式（1.8节的例7）及相似性定理。将上面二式代入式（2.6.2），得

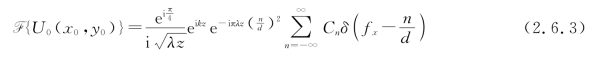
对于频率为的平面波分量，在观察平面上仅引入相移。当距离z满足条件：

(www.xing528.com)

时，则有

于是，不同频率成分在观察平面上引起的相移除了一个常数因子外，都是2π的整数倍。在这一特殊情况下，

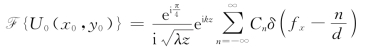
对上式作傅里叶逆变换，得到观察平面上的光场复振幅分布为

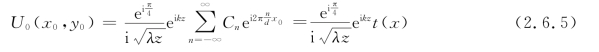
强度分布为

若不计无关紧要的常数因子，则像强度分布与物强度分布相同。于是在zT=的整数倍的距离上可以观察到物体的像。zT称为泰保距离（Talbot Distance），如图2.6.1所示。例如，物体是周期d=0.1 mm的光栅，照明光波长λ=5×10-4mm，可计算出zT=40 mm。于是在z=40 mm，80 mm，120 mm，…位置上可观察到傅里叶成像效应。

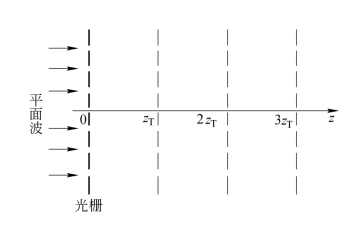
图2.6.1　泰保效应示意图

如果在光栅所产生的泰保自成像后面放一块周期相同的检测光栅，则可以观察到清晰的干涉条纹，称为莫尔条纹（MoiréFringe，详见第9章）。在上述两个光栅之间若存在位相物体，则由莫尔条纹的变化，可测量到物体的位相起伏。这就是泰保干涉仪的基本原理。

显然，凡具有周期结构的物体都有可能产生泰保效应。但由于泰保效应是衍射成像，这就要求各衍射分量之间应有正确的位相关系，即只有在相干光照明下才有可能实现。