夫琅和费衍射的正弦位相光栅|信息光学理论与应用

正弦型位相光栅的透过率函数定义为

式中，rect的作用与正弦型振幅光栅的情况相同。前面的位相因子中的位相既可以取正值也可取负值，当然作为光学厚度来说，是不能取负值的。由于位相零点的选取有着很大的任意性，所以适当选取位相参考点后，就可以把光波通过位相光栅时的平均位相延迟（常位相因子）略去。参数m体现位相正弦变化的幅度。这种正弦型位相光栅是完全透明的，它只对入射光波按式（2.5.30）引起位相延迟，对其振幅不产生衰减。

当用单位振幅的单色平面波垂直照明此光栅时，观察平面上的衍射光场分布为

为了求得t（x1，y1）的傅里叶变换，可利用贝塞尔恒等式，先对位相因子进行变换：

即

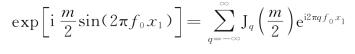
式中，Jq是q阶第一类贝塞尔函数，因其宗量不包含变量x1，故进行傅里叶变换时可以作为常数处理，于是有

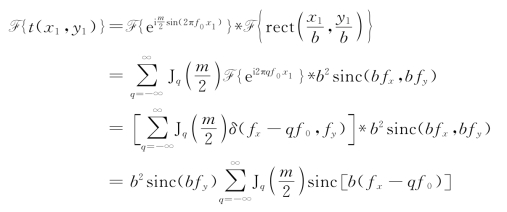
将上式代入式（2.5.31），并令，得

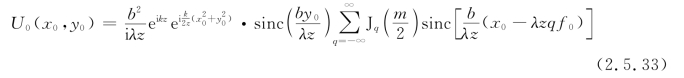
式中，q代表各衍射级次。可以看出，全部衍射级次都有可能出现。各级衍射极大值出现的位置由x0-λzqf0=0（q=0，±1，±2，…）决定，从而有(www.xing528.com)

x0=0,±λzf0,±2λzf0,…

第q级衍射极大距条纹图样中心的距离为λzqf0，相邻两级衍射分量极大值之间的距离为λzf0，每个衍射级中央最大值的宽度为。因此，只要λzf0≫，即f0≫时，不同衍射级次之间交叉相乘的各项可以忽略，这样衍射强度分布可写成

图2.5.13是正弦型位相光栅夫琅和费衍射花样沿x0轴方向规一化强度分布示意图，图中m=8。从图中看到，由于正弦型位相光栅的引入，可把能量从零阶分量转移到许多更高阶的分量上去。因此，零阶衍射分量的强度不一定最大，非零阶衍射分量的强度有可能比零阶衍射还大。只要是零阶贝塞尔函数J0的一个根，零阶条纹就完全消失！同样，当选择为某一阶贝塞尔函数的根时，其对应阶的衍射便消失了。对于已确定的m值，q增大到一定程度后，总有趋近于0，所以会限制任意高阶衍射级的使用。图2.5.14画出了3个不同q值的对的关系。

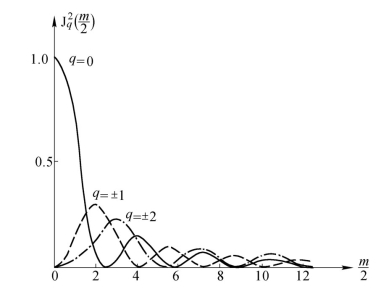
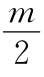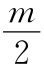图2.5.14　对于±q的3个数值，Jq2（）对的关系

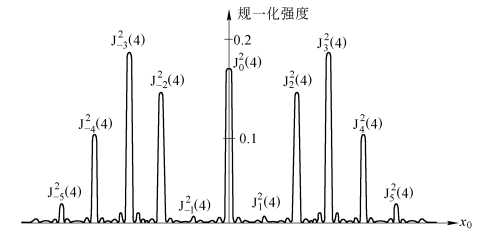
图2.5.13　一个正弦型位相光栅（m=8）的夫琅和费衍射图样的截面图

由于零级衍射分量的色散和分辨本领为零，因此正弦型位相光栅这种能使零阶衍射能量向高阶次衍射分量转移的特点，正是它优于正弦型振幅光栅和矩形光栅之处。可以证明（参见习题2.5）正弦型位相光栅的分辨本领为

即该光栅的分辨本领与测量中所用的衍射阶次以及光栅上条纹的总数目成正比。

近年来，随着衍射光学元件的发展，人们对位相光栅的研究兴趣日益增大。亚波长量级的位相光栅也引起了人们的关注。