正弦光栅夫琅衍射信息光学

前面讨论的夫琅和费衍射都是由无穷大不透明屏上的孔径产生的，其透过率函数都具有下列形式：

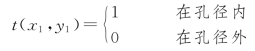
但也可以在给定的孔径内引入一个预先给定的透过率函数。换言之，可以把孔径的概念推广到一般透明或半透明的平面型物体，其透过率函数一般是复函数，光波通过该物体时，其振幅和位相分布都要受到物体的调制，使透射光波携带物体信息向前传播。例如，在特殊情况下，物体可以是一张照相底片，用以引入空间的吸收图样，它只改变入射光波的振幅分布，而不改变其位相分布，称这类物体为振幅型物体。也可以通过厚度可变的透明物体引入空间的位相图样，它只改变入射光波的位相分布，而不改变其相对振幅分布，称这类物体为位相型物体。

作为上述衍射物的典型例子，下面分别讨论正弦型振幅光栅和正弦型位相光栅。正弦型振幅光栅的透过率函数定义为

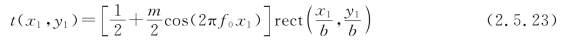
式中，f0是光栅的空间频率；m是小于1的正数；表示边长为b的正方形孔，其孔外透过率处处等于零。方孔内沿x1轴方向的透过率按正弦（或余弦）规律变化，其函数关系为，如图2.5.11所示。对于同一x1值，尽管y1值不同，但透过率是相同的。当用单位振幅的单色平面波垂直照明此光栅时，观察平面上的夫琅和费衍射光场分布为

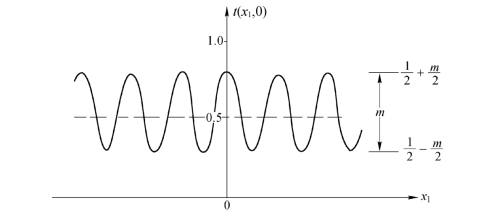
图2.5.11　正弦型振幅光栅的透过率函数

其中

将代入上式得

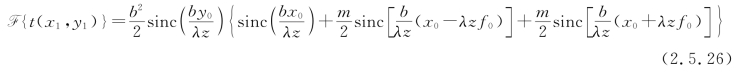
上式大括号{}内包含了3个sinc函数，中央最大值的宽度均为，第2个、第3个sinc函数由向x0轴正、负方向分别移动λzf0得到。当λzf0≫时，这两个sinc函数最大值距原点的间距比sinc函数中央最大值的宽度大得多，从而这3个sinc函数之间的重叠可忽略不计，亦即任一sinc函数与其他两个sinc函数的交叉乘积均可以忽略。于是，将式（2.5.25）代入式（2.5.24）并求光强度分布，最后可得

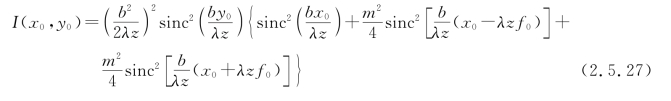
由于上式成立的条件是λzf0≫，即，而是正弦光栅的空间周期，即光栅常数，所以，要求光栅总宽度比光栅常数大得多。

图2.5.12是正弦型振幅光栅夫琅和费衍射花样沿x0轴方向的规一化光强分布示意图。可以看到，正弦振幅光栅将中央衍射图样中的一部分能量转移到附加的两个边旁图样中去了。中央衍射图样称为夫琅和费衍射的零级分量，而两个边旁图样分别称为±1级分量。零级分量到±1级分量之间的空间距离为λzf0，而每个分量的中央主极大宽度为。

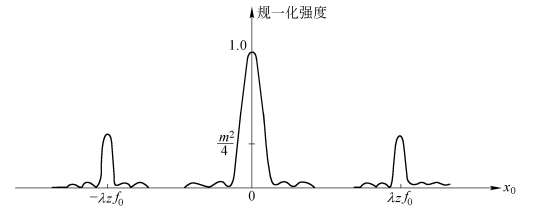
图2.5.12　正弦型振幅光栅的夫琅和费衍射强度分布(www.xing528.com)

在光学信息处理技术中，光栅常用作编码元件对图像进行空间调制。例如，设有一图像，其复振幅透过率为f（x1，y1），经光栅调制后的透射光场复振幅可以表示为

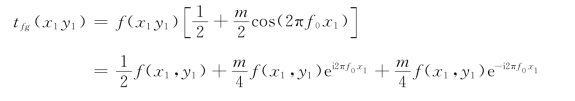
上式表明：在某方向单色平面波照射下，透射光波将携带图像信息f（x1，y1）向3个不同方向传播；用光栅进行编码，对图像作空间调制的结果是对原图像施加了不同方向的空间载波，增加了信息传递的通道。

在频率域中，透射光场的频谱为

由于光栅的调制使图像的频谱在频谱面上重复出现，除原点附近仍有图像频谱外，在（±f0，0）附近亦出现频谱。在频谱面上对图像频谱进行加工改造和处理，便是空间滤波和光学信息处理的任务。

下面分析正弦型振幅光栅的色散和分辨本领。由上面的分析知道，正弦型振幅光栅的夫琅和费衍射只有零级和±1级分量。所有波长的零级分量的极大值都位于x0=0处，所以零级分量的色散和分辨本领都是零，光栅用作分光元件时，零级分量是没有用处的，它只是损耗一部分能量，故下面只需分析±1级分量的线色散和分辨本领。

线色散表征光栅将不同波长的同级主极大在空间分开的程度。+1级极大值的位置由方程

x0-λzf0=0

确定，故其线色散为

故线色散与观察距离及光栅常数有关。

分辨本领是指分辨两个波长很靠近的谱线（λ，λ+Δλ）的能力，通常用R=表示。设波长λ和λ+Δλ的+1级谱的峰值分别位于λzf0和（λ+Δλ）zf0，则由瑞利判据，刚好能分辨的情况为一个波长的+1级谱的强度极大值位置与另一个波长的+1级谱的强度极小值位置重合，即

整理后得光栅分辨本领为

式中，N为光栅条纹总数。可见正弦型振幅光栅的分辨本领由光栅的总条纹数决定，而与观察距离z无关。