夫琅和费衍射在信息光学中的应用

光学仪器大多使用圆形光阑，它的无像差成像可以用圆形孔径的夫琅和费衍射求出，故圆孔衍射的结果是很有用的。圆孔的透过率函数为

式中，d代表圆孔的直径；r1是孔径平面上的径向坐标。对于圆对称函数，公式（2.4.13）中的傅里叶变换应改写成傅里叶-贝塞尔变换。于是，当用单位振幅的单色平面波垂直照明时，观察平面上的衍射光场可表示成

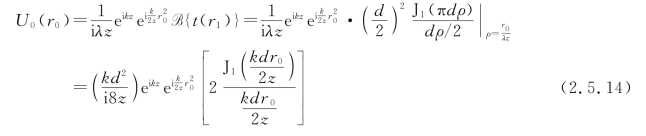
衍射光强度分布为

或简写成

式中，。

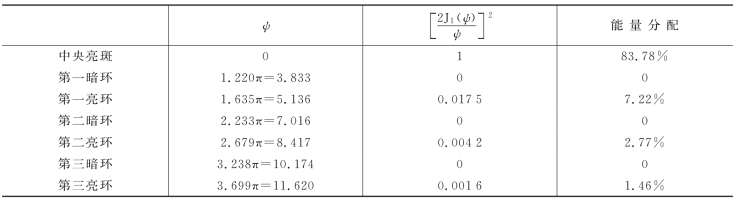
图2.5.8（a）是圆孔夫琅和费衍射花样强度分布的截面图，图2.5.8（b）是在观察面上拍摄的夫琅和费衍射图样。表2.5.1列出了衍射花样能量分布情况及其在极大点和极小点处的数值。公式（2.5.15）表示的强度分布，一般以首先导出它的科学家艾里（S.G.B.Airy，1801—1892年）命名，称为艾里函数，相应的衍射图样称为艾里衍射图样（Airy Diffraction Pattern）。在整个观察面上，艾里图样呈对称分布，是一组明暗相间的同心圆环，中央亮斑称为艾里斑（Airy Disc），其半径为

表2.5.1　圆孔的夫琅和费衍射花样能量分布

(www.xing528.com)

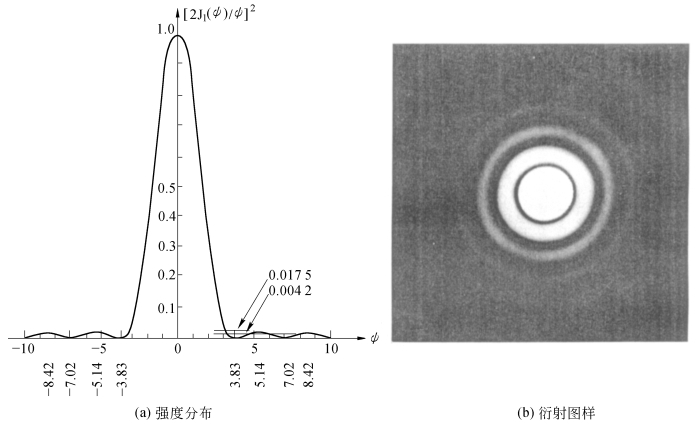
图2.5.8　圆孔的夫琅和费衍射

或写成半角宽度为

【例1】He-Ne激光器沿管轴发射定向光束，其出射窗口的直径约为1 mm，求激光束的衍射发散角。

【解】He-Ne激光的波长λ=632.8 nm，d=1 mm。由于光束受出射窗口限制，它必然会有一定的衍射发散角。由式（2.5.18）算得

这个衍射发散角虽然很小，但是，如果我们在10 km以外接收此光束的话，则由式（2.5.17）算得这束定向光束的光斑半径可达7.7 m！这个例子告诉我们，由于衍射效应，截面有限而又绝对平行的光束是不可能存在的。例如，在空间光通信和激光测距这类远程装置里，即使很小的发散角也会造成很大面积的光斑。在估算整机的接收灵敏度时，需要考虑到这一点。

计算还表明，圆孔衍射图样中央亮斑内的光能量集中了总入射光能的84%，第二暗环以内的光能流已集中总光能流的90%以上（参见习题2.3）。但必须指出，在中央亮斑以外，总光能仍具有相当大的数值（约占16%），它会产生某种程度的像寄生光，这对形成有用像是没有贡献的，因而在实验上要想办法缩减衍射环。